Basisvaardigheden rekenen/wiskunde moeten geoefend en onderhouden worden. Dat kan goed met de computer. Het Groningse onderzoeksinstituut gion onderzocht het effect van de Wiskie oefenprogramma's voor de brugklas vbo en mavo. Egbert Harskamp rapporteert over de uitkomsten van het onderzoek.
Wiskie onder de loupe
De schermafdrukken in het originele artikel zijn vervangen door Applets, die niet in alle gevallen (bijv. de Getallenfabriek) hetzelfde uiterlijk hebben.
Wiskie onder de loupe
Inleiding
Veel leerlingen in de brugklas hebben problemen met de basisvaardigheden rekenen en wiskunde. Om het inslijpen van basisvaardigheden te bevorderen, is een computerprogramma ontwikkeld door vakdidactici van het Freudenthal Instituut in samenwerking met docenten wiskunde. Het programma heet Wiskie en bestaat uit een serie oefenprogramma's (onder het kopje "Lesmateriaal" op het Wisweb gratis te downloaden).
Er zijn nog niet zoveel geschikte computerprogramma's voor rekenen en wiskunde in de basisvorming. Er is bijvoorbeeld software behorend bij de Wageningse methode met onder andere onderdelen over breuken, procenten en verhoudingen en over getallen en bewerkingen (rekenrobots). Ook zijn er enkele programma's van andere uitgevers over deze onderdelen van de leerstof. Voor het leren interpreteren van grafieken is er aardige software als Grafiekentaal van uitgeverij
nib
en
vu
-Grafiek van Wolters-Noordhoff. Het ontbreekt echter aan programma's voor het schatten van uitkomsten van bewerkingen of voor het leren oplossen van opgaven over oppervlakte of inhoud. Wiskie biedt leerlingen gevarieerde oefeningen over schatten, werken met getallen, oppervlakte en grafieken. De oefeningen worden als spelletjes aangeboden in aardig aangeklede oefenvormen, waarbij de leerling punten kan halen en waar leerlingen met en tegen elkaar kunnen spelen. De bedoeling is dat de leerlingen hun eigen oplossingsstrategieën verbeteren. De docent speelt daarbij een cruciale rol. Die kan leerlingen, via gesprekken en het stimuleren van onderling overleg, bewust maken van de mogelijkheden om opgaven efficiënt aan te pakken.
Door het Groningse onderzoeksinstituut
gion
is in het kader van het `Kortlopend Onderwijsonderzoek' bestudeerd hoe Wiskie op effectieve wijze in de praktijk van
vbo
en
mavo
kan worden toegepast. Uit het onderzoek komt naar voren dat Wiskie goed bruikbaar is en resultaten bij leerlingen oplevert. In de onderzochte praktijksituaties is veel aandacht besteed aan leerlingen die moeite hebben met rekenen en wiskunde. Wiskie biedt oefenstof voor zowel goede als zwakke rekenaars.
Wiskie
Wiskie bevat oefenspellen die zijn bedoeld als afwisseling van de oefeningen in de wiskundemethode. De leerlingen kunnen dit programma gebruiken nadat de betreffende onderdelen in de methode aan de orde zijn geweest. Wiskie is vooral bedoeld voor het oefenen van oplossingsstrategieën die leerlingen begrijpen. Het gaat dus niet om het mechanisch trainen van vaardigheden, maar om het trainen van vaardigheden waarvan de onderliggende begrippen een deel van het kennisrepertoire van leerlingen uitmaakt.
Wanneer leerlingen geen toereikende oplossingsstrategie tot hun beschikking hebben, kan de docent, via interactieve gesprekken, daarvoor zorg dragen. In hoeverre dit ook lukt met leerlingen in het
vbo
, is één van de vragen van dit onderzoek.
De belangrijkste oefenspellen in Wiskie zijn:
-
Schatten (hoofdbewerkingen procenten, kommagetallen en breuken)
-
Getallenfabriek (met getallen voorgegeven antwoorden proberen te bereiken)
-
Oppervlakte (bedekken met vierkanten en driehoeken)
-
Grafieken (interpreteren van grafieken met een of twee variabelen).
Daarnaast zijn er oefenspellen voor: de tafels van vermenigvuldiging (een bingospel), kijkmeetkunde (aanzichten van torens op een eiland), de exploratie van lineaire functies (Bollen schieten) en het memoriseren van reken/wiskundekennis (Weetjesquiz).
Het onderzoek heeft zich gericht op de eerste vier oefenspellen. De overige spellen zijn gebruikt als extra oefenstof voor de zwakke leerlingen (tafels oefenen) of voor leerlingen die sneller klaar waren met hun opdrachten.
Schatten
Bij het spel Schatten gaat het om het benaderen van de uitkomst van opgaven op het gebied van de bewerkingen tot 1000 (optellen, aftrekken, vermenigvuldigen, delen, breuken en procenten). De antwoordtijd is instelbaar. In het onderzoek is gekozen voor 20 seconden.
Er zijn vier niveaus: optellen en aftrekken, vermenigvuldigen en delen, procenten en breuken en allerlei. Soms is het mogelijk om in korte tijd een exact antwoord uit te rekenen, anders moet je getallen afronden en met afgeronde getallen rekenen.
Kies de gewenste Instellingen en klik op Start voor het spel
In het voorbeeld staat de opgave 90% van 912. De leerlingen kunnen dit uitrekenen als `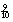 van 900 en dat is 9
¥
90'.
van 900 en dat is 9
¥
90'.
Om hoge scores te halen, moet je niet alleen kunnen schatten, maar ook kunnen compenseren binnen je schatting. In het voorbeeld hierboven zal je dus ook nog 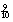 van 12 moeten schatten. En daarmee wordt het onthouden van de tussenuitkomsten niet eenvoudiger. In het onderzoek is als criterium gesteld dat de leerlingen door snel schatten in tien beurten 250 punten moesten halen.
van 12 moeten schatten. En daarmee wordt het onthouden van de tussenuitkomsten niet eenvoudiger. In het onderzoek is als criterium gesteld dat de leerlingen door snel schatten in tien beurten 250 punten moesten halen.
Getallenfabriek
Een opgave zou kunnen zijn: Maak 25 met de getallen 10, 8, 8 en 6
Het oefenspel in Wiskie bestaat uit de onderdelen:
-
Klik op een blaadje
-
Pluk een blaadje (in weze identiek aan de applet Getallenfabriek hierboven)
-
Pluk alle blaadjes
-
Flippospel.
Het gaat om handig rekenen met getallen en bewerkingen om dichtbij of op een bepaald doelgetal te komen. Bij het spel `Klik op een blaadje' mag je elk getal zo vaak gebruiken als je wilt. Bij `Pluk een blaadje' mag je alle getallen een keer gebruiken, maar het hoeft niet. Moeilijker is `Pluk alle blaadjes' waar je verplicht bent alle vier getallen te gebruiken. Bijvoorbeeld de opgave uit figuur 2: 25 maken met 10, 8, 8 en 6. Veel leerlingen zullen volstaan met de som 10 + 8 + 8 - 6 en weinig punten krijgen. Dichter bij het doelgetal is: eerst 8 + 8 = 16 en dan 16 : 6
¥
10 = 26,6666. We zien hier dat de opgaven niet altijd een precies antwoord kennen. Vooral in de spellen `Pluk alle blaadjes' en `Flippospel', waar bij elk van de vier getallen één keer moet worden gebruikt, komt het aan op inzicht in bewerkingen en op hoofdrekenen tot 100. Snelheid speelt in dit spel geen rol. Als criterium is gesteld dat leerlingen in tien beurten 30 tot 40 punten moesten behalen.
Oppervlakte
Er zijn verschillende manieren om de oppervlakte van figuren in een rooster te bepalen. De leerlingen moeten de rechthoekstrategie en driehoekstrategie kennen om de verschillende opgaven vlot op te lossen. De rechthoekstrategie voor figuren in een rooster komt veelvuldig aan de orde in de basisschool. De rechthoek- en driehoekstrategie worden in de brugklas van
mavo
en
vbo
opnieuw behandeld. In het spel krijgen leerlingen achter elkaar vijf figuren in een rooster. De leerlingen kunnen hulp aanklikken om de strategieën goed toe te passen. Daarvoor moet de figuur worden ingedeeld in meerdere stukken (rechthoeken en/of driehoeken). Het programma geeft desgewenst ook de grootte van de rechthoeken en driehoeken weer en telt de uitkomsten voor je op.
Bepaal de oppervlakte van de figuur op het rooster
In het voorbeeld hierboven zien we een rode driehoek in een rooster. Om de driehoek past een rechthoek, waaruit je vervolgens weer twee driehoeken kunt halen om de oppervlakte van de oorspronkelijke driehoek uit te rekenen. Natuurlijk kan het ook met de formule:
Opp. driehoek = b
¥
 h.
h.
Als criterium is gesteld dat leerlingen in vijf beurten tenminste 20 punten moesten behalen.
Grafieken
In dit spel beantwoorden de leerlingen steeds vier meerkeuzevragen over een beschrijvende grafiek.
Meerkeuzevragen bij een grafiek
In de tekst bij de grafiek moet op vier plaatsen iets ingevuld worden. Door op de vlakjes in de tekst te klikken, worden de antwoordalternatieven zichtbaar. De grafiek van figuur 4 gaat over een fietstocht, met op de verticale as de afstand en op de horizontale as de tijd. Maar een grafiek kan bijvoorbeeld ook gaan over het temperatuurverloop gedurende een dag. De vragen hebben betrekking op het verloop van de grafiek, over stijg- en daalpunten en over verschillen tussen punten op de grafiek. Leerlingen moeten de grafiek en de tekst van de vragen aandachtig lezen om antwoorden te kunnen geven. Ze moeten de schalen van de x-as en y-as goed leren lezen en interpreteren. Als criterium is gesteld dat leerlingen ten minste tien van de dertien grafieken moesten afmaken in een les.
Het onderzoek in de klas
Het onderzoek naar de toepassing en de effecten van Wiskie is uitgevoerd op het Katholiek Drents College te Emmen. Vooraf is nagegaan of op deze school voldoende geschikte computers beschikbaar zijn om met klassen regelmatig aan Wiskie te kunnen werken. Dit bleek inderdaad het geval. Het onderzoek is uitgevoerd vanaf half september tot begin december. De school maakt gebruik van de methode Wiskundelijn.
Er zijn twee onderzoeksgroepen gevormd uit tweede klassen
mavo
en
vbo
:
-
een experimentele groep, bestaande uit een
mavo
-klas en twee
vbo
-klassen (59 leerlingen). Deze groep kreeg gedurende de onderzoeksperiode les met Wiskie. Per week was er een les met Wiskie en waren er twee gewone wiskundelessen.
-
een controlegroep bestaande uit een
vbo
-klas en een
mavo
- klas (43 leerlingen). Deze groep kreeg drie gewone wiskundelessen per week.
Aan de klassen die met Wiskie werken, geeft een zelfde docent les, terwijl aan de andere klassen een andere docent lesgeeft.
Een les met Wiskie
Dit lesverslag is van de tweede les die de
mavo
-klas met Wiskie kreeg. Het verslag geeft een goed beeld van hoe de lessen zijn verlopen. Er zijn 25 leerlingen in deze klas. In de eerste les is al een begin gemaakt met Schatten en in deze les komt daar Grafieken bij. Bij het begin van de les worden de computers in het computerlokaal aangezet en de leerlingen pakken hun diskette. De docent zorgt ervoor dat alle leerlingen gelijktijdig met Wiskie starten. De leerlingen beginnen met het spel Schatten. De leerlingen krijgen als opdracht om 250 punten te halen bij elk van de spelniveaus (optellen en aftrekken, delen en vermenigvuldigen, breuken en procenten). De leerlingen stellen zich eerst erg afhankelijk op: `Wat te doen bij 245 punten, hoe vaak moet je het overdoen, hoe moet deze som, hoe klik je een hoger niveau aan, enzovoort'. De docent geeft korte antwoorden en laat leerlingen elkaar helpen. De docent benadrukt dat het om een oefenspel gaat en herhaalt een aantal aanwijzingen uit de vorige les:
-
heb je nu geen 250 punten dat geeft niet, dan doe je het nog een keer
-
let op hoe je handig rekent: eerst afronden op tiental of honderdtal en dan rekenen
-
neem even de tijd om af te ronden: je hebt 20 seconden
-
gokken mag, ook een tweede of derde antwoord, maar je moet dan wel snel de antwoorden intypen, want je hebt weinig tijd.
De leerlingen hebben weinig problemen met het programma. De negatieve scores als hun antwoord ver afwijkt van het goede antwoord, vinden ze gek. De docent zegt: `Geeft niet, je hebt altijd een nieuwe kans.' (In het registratiesysteem wordt bij een negatief totaal aantal punten, het totaal als 0 punten weggeschreven.)
Intermezzo 1
Het optellen en aftrekken gaat vlot. Problemen ontstaan voor sommige leerlingen bij het delen. Vijf leerlingen (drie meisjes en twee jongens) hebben echt moeite met de opgaven. De docent neemt hen apart, nadat ze het eerst zelf met Wiskie hebben geprobeerd. Het gaat in het intermezzo om compensatie van ontbrekende basisvaardigheden. De leerlingen weten niet hoe ze `een handige som' moeten zoeken bij delen en vermenigvuldigen. Bijvoorbeeld bij 300 : 8 zoek je binnen de tafel van 8 naar een deeltal dat in de buurt ligt en een mooie uitkomst geeft: 40
¥
8 = 320. Je neemt dus de deelsom 320 : 8 = 40. In Wiskundelijn wordt deze stof in het tweede leerjaar behandeld. Dit onderdeel is nu nog niet aan de orde geweest. Voor de betere leerlingen die ook even meeluisteren zegt de docent: `... maar dat is wat te veel, dus ik doe er 20 : 8, is ongeveer 2, van af. Een preciezer antwoord is 38'. Bij vermenigvuldigen hoef je alleen handig af te ronden. Bijvoorbeeld 37
¥
7. De docent zegt: `Rond het eerste getal op een tiental af. Wat krijg je dan?' Een leerling komt op 40
¥
7. Dit levert een grove schatting, waarvoor Wiskie maar weinig punten geeft. Docent: `Wat kan er dan nog af?' De zwakke leerlingen weten het antwoord hierop niet. Ze kunnen het afronden wel volgen, maar het achteraf compenseren van een schatting vinden ze erg moeilijk. Dat er van de geschatte uitkomst 3
¥
7 af kan, is alleen aan de betere leerlingen besteed. Behalve gebrek aan vaardigheid in handig rekenen, speelt bij de zwakke leerlingen ook mee dat ze inefficiënte oplossingsstrategieën gebruiken. Bijvoorbeeld 37
¥
7 wordt hoofdcijfe-rend opgelost: eerste 7
¥
7 (9 opschrijven en 4 onthouden) en dan 7
¥
3 en 4 voor de tientallen erbij. Een dergelijke aanpak gaat vaak fout of duurt te lang. De docent heeft het (grof) schatten aanbevolen voor de zwakke leerlingen.
Hierna gaan de leerlingen weer tien minuten aan de slag. De meeste leerlingen hebben daarna een voldoende niveau (250 punten) bereikt. Opvallend is dat zwakke leerlingen vaak afwisselen tussen enerzijds afronden en schatten en anderzijds hoofdcijferen. Tijdens het werken met Wiskie rekenen sommige leerlingen met hun vingers om het hoofdcijferen te ondersteunen: 37
¥
7 = eerst 9 opschrijven en 4 op de vingers zetten, daarna 21 en 4 erbij doen en ten slotte 25 opschrijven. De nadruk die leerlingen op hoofdcijferen leggen, komt waarschijnlijk omdat het spel Schatten veel punten geeft voor een precies antwoord. Het rekenen met afgeronde getallen (zonder compenseren) levert volgens de leerlingen meestal te weinig punten om in tien beurten 250 punten te halen. De leerlingen vinden strategieën als `schatten met compenseren voor afrondingen' of `handig rekenen' vaak moeilijker dan `hoofdcijferen'. Bovendien hebben ze het idee dat hoofdcijferen sneller gaat.
Intermezzo 2
Bij de breuken/procenten aangekomen, lopen de vijf leerlingen weer vast. Ze halen de 250 punten bij lange na niet. Een opgave als 75% van 663 is voor hen te moeilijk. Drie leerlingen claimen dat ze deze stof niet op de basisschool hebben gehad. De stof is nog niet in de methode aan de orde geweest. De docent geeft een korte klassikale instructie, waarbij procenten worden gekoppeld aan breuken, net als in de methode. Voor Wiskie is vooral van belang dat leerlingen kunnen rekenen met 25% = 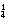 deel (delen door 4) en 10% =
deel (delen door 4) en 10% = 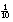 deel (delen door 10). De docent bespreekt 10% van f 663,- is f 66,30. 70% is dus zeven keer zoveel, is ongeveer 7
¥
f 70 (naar boven afgerond) is f 490,-. (Dit soort opgaven komen vooral in deel 2 B van Wiskunde Lijn aan de orde.)
deel (delen door 10). De docent bespreekt 10% van f 663,- is f 66,30. 70% is dus zeven keer zoveel, is ongeveer 7
¥
f 70 (naar boven afgerond) is f 490,-. (Dit soort opgaven komen vooral in deel 2 B van Wiskunde Lijn aan de orde.)
Met de zwakke leerlingen oefent hij nog met 50% = 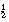 en 25% =
en 25% = 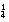 . De docent probeert de opgave 75% van 663. Voor de zwakke leerlingen wordt dit toch erg moeilijk, omdat ze eerst 75% als 3/4 moeten herkennen en dan
. De docent probeert de opgave 75% van 663. Voor de zwakke leerlingen wordt dit toch erg moeilijk, omdat ze eerst 75% als 3/4 moeten herkennen en dan 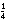 deel nemen van 663. Voor 663 : 4 moeten ze vervolgens eerst een `handige tafel' zoeken (afronden naar 640 : 4). Dit is voor hen niet te doen. De docent besluit het anders aan te pakken en zegt: `Hoeveel is 50% van 663 ongeveer? Hoeveel is 100% van 663? En hoeveel is dan 75% van 663?' Hij zet, net als in de methode, de schattingen in een overzicht.
deel nemen van 663. Voor 663 : 4 moeten ze vervolgens eerst een `handige tafel' zoeken (afronden naar 640 : 4). Dit is voor hen niet te doen. De docent besluit het anders aan te pakken en zegt: `Hoeveel is 50% van 663 ongeveer? Hoeveel is 100% van 663? En hoeveel is dan 75% van 663?' Hij zet, net als in de methode, de schattingen in een overzicht.
De leerlingen zien nu dat 75% midden tussen 331 en 663 in moet liggen. Ze schatten eerst hoeveel het is. Daarna legt de docent het uit. Het verschil tussen beide getallen is ongeveer 330 (afgerond op tiental), dus 331 + 150 + 15 zal ongeveer 75% zijn.
Een andere lastige opgave is 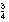 ¥
334. Ook nu weer even op het bord gezet:
¥
334. Ook nu weer even op het bord gezet: 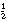 is ongeveer 170 en
is ongeveer 170 en 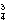 ligt tussen 170 en 334. Wat maak je ervan?
ligt tussen 170 en 334. Wat maak je ervan?
De docent laat leerlingen ook wat voorbeelden noemen uit Wiskie die ze op hun kladblaadje hebben geschreven. Resultaat van de bespreking is dat deze leerlingen wat meer durven. Helemaal snappen doen ze het nog niet. Ze schatten echter gerichter en zijn niet meer zo bang voor de tijdklok in Schatten.
Conclusies uit de lesbezoeken
Na het bezoeken van verschillende lessen waarin leerlingen van
mavo
en
vbo
met Wiskie werkten, zijn de volgende conclusies te trekken.
Gebruiksgemak
Wiskie heeft een groot gebruiksgemak voor een groot deel van de leerlingen en het programma is zelfstandig te gebruiken als de leerlingen oefeningen doen die passen bij hun beheersingsniveau. Toch moet de docent veel extra uitleg geven, omdat zwakkere leerlingen kennis en vaardigheden missen om de oefeningen voldoende te kunnen maken.
Passing bij de methode
De uitleg in de methode Wiskunde Lijn past bij de oefeningen van Wiskie. Een probleem was dat sommige leerstofonderdelen nog niet voldoende in de methode aan de orde zijn geweest op het moment van het onderzoek.
Interactie docent en leerlingen
Het werken met Wiskie vereist dat de docent steeds aanwezig is om leerlingen verder te helpen. Vooral zwakke leerlingen hebben steun en stimulering nodig om vol te houden. Uitleg en bespreking van oplossingen met subgroepen bleek in de onderzochte klassen het meest geschikt. Klassikale bespreking van oplossingswijzen werkt niet goed. De betere leerlingen vinden veel van de oplossingswijzen `basisschoolstof' en de zwakke leerlingen vinden het niet zo prettig om voor de hele klas over hun (half goede) oplossingen te praten.
Werkwijze van de leerlingen
Over het algemeen hebben zwakke rekenaars moeite met een goede aanpak. Ze passen bij Schatten bijvoorbeeld grove schatmethodes toe of ze gaan juist heel precies en mechanisch rekenen (cijferen). De docent is vooral ingegaan op efficiënte aanpakken. De indruk uit de observaties is dat leerlingen, mede door de beloningsstructuur in Wiskie, vooral het exacte antwoord willen geven. Dit geldt zowel voor Schatten als voor Getallenfabriek. In de spellen Grafieken en Oppervlakte moeten de leerlingen een precies antwoord geven.
Samenwerken
Het samenwerken van leerlingen gaat heel functioneel: help me eens! De spellen lenen zich niet echt voor onderling overleg over oplossingen. Het gaat in Wiskie vooral om oefening en beloning van de individuele vaardigheid.
Evaluatie
Het stellen van een beheersingscriterium werkte goed. Op die manier signaleerden de leerlingen en de docent sneller waar ze problemen hebben. Het zou makkelijk zijn als er in het scherm van de leerlingen een registratie van de vorderingen van leerlingen tijdens de les werd bijgehouden. Nu komt de registratie van leerlinggegevens achteraf en zien leerlingen zelf het resultaat niet. Het registratiesysteem geeft namelijk gegevens per klas (alle leerlingen onder elkaar) en per les en niet per leerling.
Resultaten van de leerlingen
Om na te gaan welke verbeteringen zich voordoen bij leerlingen die met Wiskie oefenen, zijn aan het begin en het einde van het onderzoek in september en december 1998 toetsen afgenomen bij de leerlingen. De toetsen hebben vier onderdelen. We geven enkele opgaven uit de natoets als voorbeeld.
Schatten
In dit onderdeel worden leerlingen gevraagd om getallen af te ronden en om schattingen te maken met de hoofdbewerkingen. Dit lijkt op de oefeningen in Schatten, maar dan zonder tijdslimiet en met multiple-choice antwoorden. Een voorbeeld:
Getallen en bewerkingen
In dit onderdeel gaat het om het maken van een opgave met meerdere bewerkingen door het invullen van getallen. Dit lijkt op de oefeningen in Getallenfabriek, maar ook op opgaven in de wiskundemethode. Een voorbeeld:
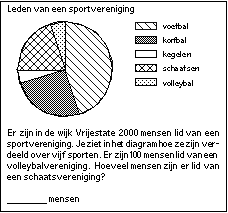
Grafieken
Het aflezen en interpreteren van grafieken met een variabele (cirkeldiagram) of twee variabelen (lijn- of staafgrafiek). De grafieken zijn over het algemeen eenvoudiger dan die in het gelijknamige oefenspel. Een voorbeeld:
Oppervlakte
Oppervlakte van vlakke figuren tellen of berekenen met rechthoekstrategie of driehoekstrategie. De opgaven komen overeen met die in het oefenspel of in de wiskundemethode, maar in de toets is geen hulp mogelijk zoals in het oefenspel. Voorbeeldopgave:
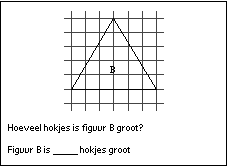
Nagegaan is of leerlingen die met Wiskie werkten betere toetsprestaties behaalden dan de overige leerlingen. Van tevoren is vastgesteld dat er op de voortoets geen verschillen waren tussen de leerlingen die met Wiskie werkten (de experimentele groep) en de leerlingen die zonder computerprogramma werkten (controlegroep).
In tabel 1 wordt een overzicht gegeven van de resultaten op de vier toetsonderdelen. In de tabel zijn de gemiddelde scores van leerlingen op de natoets van de experimentele groep vergeleken met die van de controlegroep en er is nagegaan op welke onderdelen de experimentele groep meer is vooruitgegaan. Bij het onderdeel schatten is er geen significant verschil tussen beide groepen. Op de andere drie onderdelen is er wel verschil, ieder keer in het voordeel van de experimentele groep.
-
Gemiddeld percentage goed gescoorde items op de natoets uitgesplitst naar experimentele en controlegroep
|
|
Schatten
(12 items)
|
Getallen
(8 items)
|
Grafieken*
(6 items)
|
Oppervlakte*
(5 items)
|
|
experimentele groep
(59 leerlingen)
|
77%
|
88%
|
60%
|
54%
|
|
controlegroep
(43 leerlingen)
|
75%
|
76%
|
42%
|
40%
|
De experimentele groep is op de onderdelen getallen, oppervlakte en grafieken aanzienlijk meer vooruitgegaan dan de controlegroep, maar op schatten niet. Op zichzelf is deze uitkomst positief, maar verrassend. Er is aan het spel Schatten veel aandacht besteed in de lessen, maar de resultaten zijn daarmee niet in overeenstemming.
Nadere analyse van de toetsgegevens en de gegevens over het aantal keer dat een leerling de oefenspellen heeft gebruikt, laat het volgende zien:
-
Over het algemeen is er een negatieve samenhang tussen de voortoets-resultaten en het aantal keren dat een oefenspel is gebruikt door de leerlingen. Dit betekent dat leerlingen die zwak waren (onder het gemiddelde scoorden) op de voortoets, meer hebben geoefend met Wiskie dan de betere leerlingen. Dit is overigens ook de bedoeling van het werken met een beheersingscriterium voor de oefenspellen. Liefst trainen leerlingen net zo vaak tot ze het beheersingscriterium hebben gehaald.
-
Binnen de experimentele groep is er op de natoets geen verband meer tussen het aantal keren oefenen en de toetsresultaten. Het betekent dat ongeacht het aantal keren oefenen, er betere prestaties zijn behaald door de leerlingen van de experimentele groep in vergelijking met de controlegroep. De zwakke leerlingen in de experimentele groep zijn er op de natoets relatief evenveel op vooruitgegaan als de betere leerlingen in die groep. Zwakke leerlingen hebben dus over het algemeen meer geoefend, maar hebben doorgaans evenveel leerwinst behaald als de betere leerlingen.
-
In tegenstelling tot de andere oefenspellen blijkt er bij het spel Schatten een positief verband te zijn tussen het aantal keer oefenen met het spel en de voortoetsresultaten voor schatten. Dit duidt erop dat vooral de betere leerlingen vaker het spel Schatten hebben gedaan. Op de natoets is er echter geen verband tussen het aantal keren dat Schatten is gedaan en de toetsresultaten. Dit duidt erop dat de betere leerlingen van Schatten al even weinig hebben bijgeleerd als de zwakkere leerlingen. Hieraan moet worden toegevoegd dat leerlingen wellicht sneller zijn gaan rekenen als gevolg van het spel. De natoets heeft echter niet gemeten hoe snel je kunt rekenen, maar vooral of je handig kunt afronden en schatten.
De kwantitatieve uitkomsten over de toetsresultaten bevestigen hetgeen in de observaties al naar voren kwam. Het Schatspel biedt zwakke leerlingen relatief weinig ondersteuning om ontbrekende voorkennis aan te vullen. De docent moet hen veel uitleggen over hoe je schatstrategieën kunt toepassen. Als dat niet gebeurt, leren de leerlingen niets van de oefeningen. Het spel zelf bevordert dat leerlingen precies gaan uitrekenen in plaats van schatten, ze gaan dan vaak hoofdcijferen in plaats van schatten. Kennelijk vinden de betere leerlingen het leuk om op snelheid te spelen en voor hen is Schatten aantrekkelijk. De zwakkere leerlingen vinden Schatten vaak minder leuk om te doen.
Oplossingsstrategieën van leerlingen
Bij de afname van de voortoets en de natoets is voor alle leerlingen bij vijf opgaven nagegaan hoe ze die hebben opgelost. In een vooronderzoek is door middel van interviews met 25 leerlingen van leerjaar 2 van het
vbo
onderzocht hoe deze opgaven worden opgelost. Naar aanleiding van de bevindingen in het vooronderzoek zijn bij elk van de vijf opgaven de oplossingsstrategieën opgenomen in de toetsen voor het hoofdonderzoek. Aan de hand van de strategieën zijn schriftelijke vragen gesteld over de oplossingswijze die leerlingen in de experimentele en controlegroep volgden. De vijf opgaven gaan over `schatten' en `getallen en bewerkingen'. Voor het type opgaven verwijzen we naar de voorbeeldopgaven 1 en 2 hierboven.
Op de voortoets bleken er geen verschillen te zijn tussen de leerlingen van de experimentele en de controlegroep in het gebruik van strategieën. Dit was ook niet verwacht. Naar verwachting zouden de verschillen in strategie-gebruik zichtbaar worden op de natoets. De leerlingen in de experimentele groep is tijdens de instructie en besprekingen namelijk geleerd om bij het spel Schatten eerst af te ronden en dan op te tellen of af te trekken (strategie 3). Voor het delen is hen geleerd om vooral een mooie buursom in dezelfde tafel te zoeken (strategie 2). De zwakkere leerlingen is aangeraden af te ronden en dan te rekenen met ronde en deelbare getallen (strategie 3). Bij de opgaven in de Getallenfabriek is vooral de betere leerlingen geadviseerd de opgaven redenerend op te lossen (strategie 3) en de zwakkere leerlingen om systematisch uit te proberen (strategie 2). Deze laatste strategie wordt vooral door het programma ondersteund. Kortom: het is te verwachten dat leerlingen die met Wiskie hebben gewerkt vaker strategie 3 of 2 toepassen dan leerlingen uit de controlegroep. De leerlingen in de controlegroep passen, naar verwachting, vaker strategie 1 toe of geven in het geheel geen antwoord.
-
Gemiddeld percentage van de vijf opgaven waarbij de leerlingen een bepaalde strategie gebruiken (standaardafwijkingen tussen haakjes)
|
|
Controle-
groep
|
Experimentele
groep
|
|
Geen strategie gekozen, geen antwoord
|
2% (7)
|
4% (7)
|
|
Strategie 1: hoofdcijferen en splitsend hoofdrekenen (schatten) of willekeurig proberen (getallen en bewerkingen)
|
30% (21)
|
26% (22)
|
|
Strategie 2: handig rekenen (schatten) of systematisch proberen (getallen en bewerkingen)
|
14% (13)
|
18% (18)
|
|
Strategie 3: afronden en schattend rekenen (schatten) of redeneren (getallen en bewerkingen)
|
44% (26)
|
52% (27)
|
|
|
100% van de opgaven
|
100% van de opgaven
|
De gegevens in tabel 2 laten zien dat de verschillen in strategie-gebruik tussen de experimentele en de controlegroep gemiddeld genomen erg klein zijn. De verschillen zijn dan ook niet significant. Dat komt vooral omdat er zowel binnen de experimentele groep als binnen de controlegroep zulke grote verschillen in gebruik van de strategieën zijn. De spreiding in scores van tweederde van de leerlingen voor de vijf opgaven ligt een standaardafwijking rond het gemiddelde. Voor de experimentele groep bij strategie 2 liggen de scores dus tussen 0% en 36% en voor de controlegroep tussen 1% en 27%.
We zien dat strategie 2 en 3 in de controlegroep gemiddeld bij 58% van de opgaven (bijna 3 van de 5 opgaven) wordt gebruikt en in de experimentele groep bij 70% van de opgave (bij 3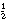 van de 5 opgaven). Er blijkt verder een duidelijk negatieve samenhang te zijn tussen de frequentie in het gebruik van strategie 1 en de natoetsresultaten (r = -.38; p < .05). Tussen de frequentie in het gebruik van strategie 2 of 3 en de natoetsscores is een positief verband (r = .26; p < .05). Deze verbanden tussen strategie-gebruik en toetsresultaten wijzen erop dat strategie 2 en 3 inderdaad aan te bevelen zijn, omdat leerlingen daarmee wat vaker tot goede antwoorden komen. Strategie 1 is af te raden. Leerlingen maken hiermee te vaak fouten.
van de 5 opgaven). Er blijkt verder een duidelijk negatieve samenhang te zijn tussen de frequentie in het gebruik van strategie 1 en de natoetsresultaten (r = -.38; p < .05). Tussen de frequentie in het gebruik van strategie 2 of 3 en de natoetsscores is een positief verband (r = .26; p < .05). Deze verbanden tussen strategie-gebruik en toetsresultaten wijzen erop dat strategie 2 en 3 inderdaad aan te bevelen zijn, omdat leerlingen daarmee wat vaker tot goede antwoorden komen. Strategie 1 is af te raden. Leerlingen maken hiermee te vaak fouten.
Vergelijking van het strategie-gebruik op de voortoets en de natoets laat zien dat leerlingen in beide onderzoeksgroepen gemiddeld genomen voorafgaande en na het experiment even vaak de drie strategieën hebben gebruikt. Er is dus in beide groepen geen vooruitgang in de zin dat strategie 2 en 3 vaker worden gebruikt. Voor schatten geldt bovendien dat leerlingen in de experimentele groep hun bestaande strategieën ook niet beter zijn gaan gebruiken. Deze leerlingen maken de schatopgaven immers niet beter dan leerlingen uit de controlegroep. Voor het onderdeel `getallen en bewerkingen' geldt dat wel. Leerlingen zijn kennelijk hun strategieën beter gaan gebruiken, want ze maken meer opgaven goed.
Onze conclusie is dat het werken met Wiskie niet heeft geleid tot frequenter gebruik van efficiënte oplossingswijzen door leerlingen, maar waarschijnlijk wel tot een beter gebruik van oplossingswijzen die leerlingen toch al gebruikten.
Aanbeveling voor het gebruik van Wiskie
Er kan aan Wiskie nog het een en ander worden verbeterd, maar dat neemt niet weg dat het programma nu reeds tot verbetering van vaardigheden bij leerlingen kan leiden. We hebben gezien dat werken met Wiskie profijt kan hebben voor de leerlingen. Het is daarom van belang om stil te staan bij de condities waaronder werken met Wiskie moet gebeuren.
We trekken uit onze ervaringen de volgende conclusies:
-
Wiskie is effectief als je er gedurende langere tijd gebruik van maakt. Aan te raden is om regelmatig, bijvoorbeeld tweewekelijks, te oefenen gedurende het cursusjaar. Nieuwe oefenspellen kunnen aan de orde worden gesteld als de leerstof in de methode wordt aangeboden. De leerstof van Oppervlakte, Grafieken en de lagere niveaus van Schatten en Getallenfabriek, komt in de tweede helft van het eerste leerjaar
vbo
en
mavo
vaak aan de orde. De leerstof voor de hogere niveaus van Getallenfabriek en Schatten in het tweede leerjaar. Wiskie kan in het tweede jaar dus continu worden gebruikt. Het is aan te raden om de oefenspellen uit Wiskie systematisch aan te bieden en de hoeveelheid oefening en het te bereiken niveau met de spellen af te stemmen op het beheersingsniveau van de leerlingen.
-
Er is onderwijs nodig voorafgaande aan en tijdens het gebruik van Wiskie. Wiskie is dus geen programma dat `los van de docent' kan worden gebruikt. Wiskie geeft geen instructie in oplossingswijzen. Vooral procenten, breuken, kommagetallen en haakjesgebruik leveren de leerlingen problemen op. Er moet steeds vooraf en tijdens het werken met Wiskie even worden stilgestaan bij de rekenaanpakken van leerlingen. Leerlingen vergeten de aanpakken erg snel: waarschijnlijk is hun kennis erg contextgebonden. Bijvoorbeeld: procenten in de les lijken andere procenten dan die bij Schatten op de computer. De docent moet, met name voor zwakke leerlingen, steeds weer het verband leggen tussen de vaardigheid zoals aangeboden in de methode en de vaardigheid zoals die met Wiskie moet worden geoefend.
-
Om leerlingen actief bij het oefenen met Wiskie te betrekken, is het aan te bevelen om leerlingen aantekeningen te laten maken van opgaven die ze moeilijk vonden. De aantekeningen van leerlingen kunnen onderwerp van extra lesjes met zwakke leerlingen zijn. Op grond van hun aantekeningen weten leerlingen vaak te vertellen hoe ze een opgave hadden willen maken. Verder is het aan te bevelen om leerlingen van ongeveer gelijk niveau naast elkaar te zetten, zodat ze elkaar kunnen helpen en samen een spel kunnen doen. Met name voor zwakke leerlingen is van belang dat ze even tussendoor kunnen overleggen om hen over hun faalangst heen te helpen.
-
Het registratiesysteem werkt goed zolang alle leerlingen dezelfde oefeningen doen. Het is niet geschikt om voor individuen overzichten te maken. Met het registratiesysteem kijkt de leraar na welke leerlingen achterblijven en geeft extra beurten en oefeningen. Een overzicht per leerling zou een verdere verbetering zijn. Je kunt de informatie per leerling wel wegschrijven en printen, maar daar is enige handigheid voor nodig.
Het starten en afsluiten van Wiskie met een diskette is wat primitief, maar blijft nodig als er nog niet onder een intern netwerk op school wordt gewerkt. Zo lang de leerlingen goed met de diskettes omgaan, werkt het systeem van oefenen en het vervolgens inlezen van de gegevens op de computer van de docent. De leerlingen moeten goed opletten om de diskette pas aan het einde van hun oefeningen uit de computer te halen.
-
Het is aan te raden om per spel een criteriumscore aan te geven voor de leerlingen. Dat is in het onderzoek ook gedaan en werkte goed. De criteriumscores kunnen variëren met het niveau van de leerling. Voordeel van een criteriumscore is dat leerlingen weten wanneer ze een spel voldoende hebben geoefend.
Het onderzoek is gefinancierd uit het budget dat het Ministerie van
oc
&
w
jaarlijks beschikbaar stelt aan de
lpc
ten behoeve van Kortlopend Onderwijsonderzoek, dat wordt uitgevoerd op verzoek van het onderwijsveld, projectnummer 97.1.4.2.
Verdere informatie over het onderzoek kunt u vinden in:
E. Harskamp en C. Suhre (1999). Software voor rekenen en wiskunde in de brugklas. Groningen:
gion
.
Te bestellen bij
gion
, mevrouw V. Mak
tel. 050-363 66 35
Prijs f 29, 95.
E. Harskamp,
gion
(Gronings Instituut voor Onderzoek van Onderwijs), Westerhaven 15, 9718 AW Groningen
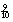 van 900 en dat is 9
¥
90'.
van 900 en dat is 9
¥
90'. 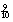 van 12 moeten schatten. En daarmee wordt het onthouden van de tussenuitkomsten niet eenvoudiger. In het onderzoek is als criterium gesteld dat de leerlingen door snel schatten in tien beurten 250 punten moesten halen.
van 12 moeten schatten. En daarmee wordt het onthouden van de tussenuitkomsten niet eenvoudiger. In het onderzoek is als criterium gesteld dat de leerlingen door snel schatten in tien beurten 250 punten moesten halen.  h.
h. 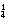 deel (delen door 4) en 10% =
deel (delen door 4) en 10% = 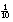 deel (delen door 10). De docent bespreekt 10% van f 663,- is f 66,30. 70% is dus zeven keer zoveel, is ongeveer 7
¥
f 70 (naar boven afgerond) is f 490,-. (Dit soort opgaven komen vooral in deel 2 B van Wiskunde Lijn aan de orde.)
deel (delen door 10). De docent bespreekt 10% van f 663,- is f 66,30. 70% is dus zeven keer zoveel, is ongeveer 7
¥
f 70 (naar boven afgerond) is f 490,-. (Dit soort opgaven komen vooral in deel 2 B van Wiskunde Lijn aan de orde.)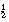 en 25% =
en 25% = 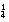 . De docent probeert de opgave 75% van 663. Voor de zwakke leerlingen wordt dit toch erg moeilijk, omdat ze eerst 75% als 3/4 moeten herkennen en dan
. De docent probeert de opgave 75% van 663. Voor de zwakke leerlingen wordt dit toch erg moeilijk, omdat ze eerst 75% als 3/4 moeten herkennen en dan 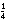 deel nemen van 663. Voor 663 : 4 moeten ze vervolgens eerst een `handige tafel' zoeken (afronden naar 640 : 4). Dit is voor hen niet te doen. De docent besluit het anders aan te pakken en zegt: `Hoeveel is 50% van 663 ongeveer? Hoeveel is 100% van 663? En hoeveel is dan 75% van 663?' Hij zet, net als in de methode, de schattingen in een overzicht.
deel nemen van 663. Voor 663 : 4 moeten ze vervolgens eerst een `handige tafel' zoeken (afronden naar 640 : 4). Dit is voor hen niet te doen. De docent besluit het anders aan te pakken en zegt: `Hoeveel is 50% van 663 ongeveer? Hoeveel is 100% van 663? En hoeveel is dan 75% van 663?' Hij zet, net als in de methode, de schattingen in een overzicht. 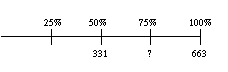
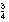 ¥
334. Ook nu weer even op het bord gezet:
¥
334. Ook nu weer even op het bord gezet: 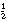 is ongeveer 170 en
is ongeveer 170 en 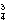 ligt tussen 170 en 334. Wat maak je ervan?
ligt tussen 170 en 334. Wat maak je ervan?

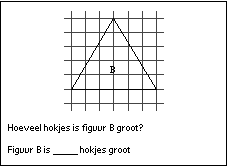
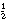 van de 5 opgaven). Er blijkt verder een duidelijk negatieve samenhang te zijn tussen de frequentie in het gebruik van strategie 1 en de natoetsresultaten (r = -.38; p < .05). Tussen de frequentie in het gebruik van strategie 2 of 3 en de natoetsscores is een positief verband (r = .26; p < .05). Deze verbanden tussen strategie-gebruik en toetsresultaten wijzen erop dat strategie 2 en 3 inderdaad aan te bevelen zijn, omdat leerlingen daarmee wat vaker tot goede antwoorden komen. Strategie 1 is af te raden. Leerlingen maken hiermee te vaak fouten.
van de 5 opgaven). Er blijkt verder een duidelijk negatieve samenhang te zijn tussen de frequentie in het gebruik van strategie 1 en de natoetsresultaten (r = -.38; p < .05). Tussen de frequentie in het gebruik van strategie 2 of 3 en de natoetsscores is een positief verband (r = .26; p < .05). Deze verbanden tussen strategie-gebruik en toetsresultaten wijzen erop dat strategie 2 en 3 inderdaad aan te bevelen zijn, omdat leerlingen daarmee wat vaker tot goede antwoorden komen. Strategie 1 is af te raden. Leerlingen maken hiermee te vaak fouten.