Een baby van 500 pond

Meisjes en jongens verschillen in rekenen

Marjolein Kool, Marja van den Heuvel-Panhuizen, Erica de Goeij

dit artikel is reeds eerder verschenen in Willem Bartjens (2000, jaargang 19, nr. 4, pp. 9-11)

Jaar in jaar uit toont de Cito Eindtoets Basisonderwijs het opnieuw aan: de gemiddelde rekenprestaties van de meisjes blijven achter bij die van de jongens. Nader onderzoek naar dit verschijnsel heeft aspecten van het reken- en wiskundeonderwijs aan het licht gebracht die voor verbetering vatbaar zijn. Deze bevindingen vormen de ingrediënten voor de module Meisjes-Jongens, die momenteel voor de Nationale Cursus RekenCoördinator (NCRC) wordt ontwikkeld.

Een rekenles in groep 8

Donderdagmorgen, rekenles in groep 8 op een doodgewone basisschool ergens in het midden van het land. Leuke meisjes, aardige jongens en een ervaren leraar met bijzonder veel belangstelling voor het vak rekenen-wiskunde. Het vraagstuk dat vandaag centraal staat is het volgende: In 1995 bezaten alle Nederlanders met elkaar 4.978.157 auto's. Dat betekent dus ongeveer 1 auto op de hoeveel inwoners? Het blijft niet lang stil in de klas. 'Je moet weten hoeveel inwoners Nederland heeft.' oppert een leerling. 'Inderdaad.' reageert de leraar, 'Wie weet hoeveel inwoners wij hebben?' Meteen schieten er tien vingers in de lucht. Allemaal jongens! Als één van hen '15 miljoen' zegt, mompelen de anderen instemmend. De leraar schrijft dat aantal op het bord en vraagt hoe het verder moet. Weer zijn er zo'n tien vingers en weer blijken het allemaal jongens te zijn. 'Je moet het aantal auto's afronden', oppert er eentje. 'Ik maak er 5 miljoen van.' De 5.000.000 auto's worden onder de 15.000.000 inwoners geschreven. 'Wat komt er dus uit het vraagstuk, Marloes?' vraagt de leraar aan een meisje dat erg haar best doet om het allemaal te volgen. Ze blijft het antwoord schuldig. De jongens staan te trappelen om haar te helpen en de leraar geeft één van hen de kans om '1 op de 3' in te koppen. De jongen legt uit hoe hij er aan komt en ondertussen zwijgen de meisjes in alle talen. Ze stellen ook geen vragen. Pas als de leraar vraagt wie 1 op de 3 in een sectordiagram kan tekenen, kruipen ze uit hun schulp. Een meisje tekent de juiste tekening op het bord. En als er even later cijferend vermenigvuldigd moet worden, blijken de meisjes minder slordigheidsfouten te maken dan de jongens.

Waar blijven de meisjes?

Deze groep 8 beantwoordt aan het beeld dat geschetst wordt in het MOOJ-rapport dat verschillen tussen meisjes en jongens bij het vak rekenen-wiskunde op de basisschool beschrijft.*1* Als het gaat om maatkennis, schattend rekenen, handig rekenen, rekenen met grote getallen en dergelijke, dan haken meisjes af. Wanneer het gaat om een standaardprocedure of vraagstukken waarbij nauwkeurig gelezen moet worden dan doen de meisjes het even goed en soms zelfs iets beter dan de jongens. Na de les blikken we terug en de leraar valt meteen met de deur in huis: 'Heb je gezien hoe het ging met de meisjes?' vraagt hij. Zo gaat het hier nou altijd in de rekenles. Ik heb absoluut slimme meiden in de klas. Bij andere vakken laten ze de jongens over het algemeen ver achter zich. Dan laten ze zich de kaas ook niet van het brood eten. Maar bij rekenen geven ze niet thuis. Het lijkt wel of ze niet durven. Terwijl ik moet zeggen dat ik erg hard werk aan een goede sfeer in de klas. De leerlingen lachen elkaar niet uit als er iemand een fout maakt. Ik heb het idee dat iedereen zich veilig voelt, maar bij rekenen blijkt dat niet genoeg te zijn.'

Meisjes rekenen anders

De ultieme oplossing voor het probleem bestaat niet. Meisjes en jongens verschillen, dat is een gegeven. In het moderne realistische reken-en wiskundeonderwijs wordt aan leerlingen vaak gevraagd om eigen oplossingen te bedenken en handige strategieën uit te proberen. Maar meisjes willen juist graag van te voren horen hoe ze een probleem aan moeten pakken, ze houden niet van schattend rekenen en ze kiezen liever een veilige standaardaanpak, zoals bijvoorbeeld een staartdeling, dan een handige oplosmanier. Van de opdracht 60 x 0,25 durven de meeste meisjes niet 60 : 4 te maken. Het komt niet in hen op om een deling te maken als er om een vermenigvuldiging gevraagd wordt.
Dat er verschillen bestaan tussen meisjes en jongens bij het vak rekenen is te accepteren. Anders wordt het echter, als die verschillen mede veroorzaakt of versterkt worden door het onderwijs. Het MOOJ-onderzoek heeft laten zien dat het rekenonderwijs op dit punt verbeterd kan worden en dat vormt natuurlijk een mooie uitdaging.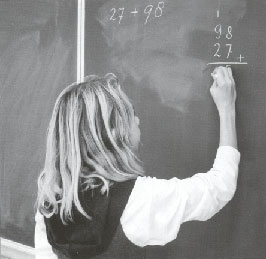




Nascholing voor leraren

Om het onderwijsveld haar voordeel te laten doen met de bevindingen van het MOOJ-onderzoek wordt er op het Freudenthal Instituut gewerkt aan de nascholingsmodule 'Meisjes-Jongens'. Het is een onderdeel van de Nationale Cursus RekenCoördinator. De NCRC-modulen zijn bestemd voor rekencoördinatoren, die de kennis en ervaringen die ze in de cursusbijeenkomsten opdoen, gebruiken om op hun school een bijdrage te leveren aan de verbetering van het reken-wiskundeonderwijs. Ze krijgen zelfs speciale thuisopdrachten om hun collega's mee te laten profiteren van de cursus. De NCRC-modulen 'Oefenen' en 'Hele Getallen Onderbouw Basisschool' zijn al klaar. De module 'Meisjes-Jongens' verkeert op dit moment in de try-out fase.
Donderdagavond, twaalf rekencoördinatoren bezoeken de Hogeschool van Haarlem om daar onder leiding van cursusleidster Lianne de Vet op zoek te gaan naar mogelijkheden om hun rekenonderwijs te optimaliseren voor meisjes (en jongens!) Het onderwerp dat deze keer centraal staat is maatkennis. Eerst wordt de eigen maatkennis verkend: Hoeveel jaar geleden leefden er dinosaurussen op aarde? Hoe zwaar is een ei? Wat kost een pak melk, een auto? Wat is de omtrek van de aarde? Wat is de kracht op de schaal van Richter van een zware aardbeving? Aanvankelijk buigen de cursisten zich in doodse stilte over de vragen, dan roept een vrouwelijke cursist giechelend: 'Ik weet helemaal niks!' Een ander valt in: 'Het enige dat ik weet is dat dinosaurussen voor Christus leefden.' Bij de nabespreking blijkt het mee te vallen. Ze heeft zojuist een tweedehandsauto gekocht, dus over de prijs van auto's kan ze aardig meepraten. De aardbeving in Turkije heeft ook niemand onberoerd gelaten, dus daar kan ook iedereen een zinnig antwoord op geven. Het gewicht van een ei weet een mannelijke cursist: 'Ik schatte eerst het gewicht van een heel doosje eieren.' En ook de omtrek van de aarde weet hij feilloos te noemen. Door deze activiteit wordt duidelijk dat maatkennis verbonden is met ervaringen en specifieke persoonlijke interesses. Een tweede try-out van de cursus wordt verzorgd door Nico Eigenhuis van het CED in Rotterdam. Zijn cursisten beweren enthousiast dat ze dankzij de cursus met nieuwe ogen naar hun leerlingen zijn gaan kijken. Een van zijn cursisten -leerkracht van groep 8- vertelde dat er bij hem op school aan groepdoorbrekend rekenonderwijs wordt gedaan: 'Ik realiseer me nu pas dat de leerlingen uit mijn klas die een groep lager rekenen, allemaal meisjes zijn.'

Jongens hebben meer oog voor getallen

Over het algemeen blijken mannen over meer losse getallenfeitjes te beschikken dan vrouwen. Op de basisschool is dat al niet anders. Jongens weten hoe hard een auto kan rijden en welk transferbedrag er voor sommige voetballers betaald wordt. 'Ja maar', zegt een cursist, 'dat zijn ook typisch mannelijke onderwerpen.' Daar blijkt het echter niet aan te liggen. De cursisten bekijken een videofragment. Aan een meisje en een jongen wordt gevraagd hoe zwaar volgens hen een pasgeboren baby is. Het meisje schat 300 tot 500 pond. De jongen zegt: '3 kilo of zo.' Ook in meer meisjesachtige contexten blijken meisjes weinig maatkennis te hebben. Het volgende videofragment toont twee meisjes uit groep 6 die menen dat er 300 dagen in een jaar zitten en dat de afstand Groningen-Maastricht 60 kilometer bedraagt. Hoe erg is het dat meisjes niet zoveel maatkennis hebben? Wie een willekeurig rekenboek openslaat ziet het antwoord.' Gebrek aan maatkennis speelt je bij zeer veel opgaven parten.' Een selectie:

- Bianca is over 6000 minuten jarig. Wanneer is dat?
- Waar of niet waar: De emmer bevat 5000 cm*3* water.
- Zet de komma op de goede plaats: een bloemkool weegt 1250 kg
- Vul in mm, cm, dm, m, km: De afstand Amsterdam-Parijs is ongeveer 500...
- Hoeveel auto's staan er in 15 kilometer file?




De opbouw van maatkennis

Bij het realistisch reken- en wiskundeonderwijs speelt het hebben van maatkennis een grote rol. Het komt bijvoorbeeld goed van pas bij het controleren van de uitkomst van een berekening op realiteitswaarde. Maatkennis is belangrijk, maar in de meeste reken-wiskundemethoden wordt het niet expliciet aangeleerd. De auteurs van de methoden gaan ervan uit dat kinderen maatkennis opdoen in het dagelijks leven. Dat gebeurt ook wel, maar het blijkt te weinig te zijn en bovendien blijkt dat meisjes als ze niet gestimuleerd worden, minder maatkennis opdoen dan jongens. De cursisten zijn het eens: Dit is een hiaat in het rekenonderwijs. Hier moet iets aan gedaan worden. En omdat de methoden het onderwerp laten liggen, zal de leraar zelf aan de slag moeten. 'Over welke maatkennis moeten kinderen op welke leeftijd beschikken?' De cursisten steken van wal: een kleuter moet zijn eigen leeftijd kennen, een kind uit groep 5 moet weten hoe hard een fietser gaat, een leerling uit groep 8 moet de afmetingen van Nederland kennen. Omgekeerd moeten leerlingen iets kunnen noemen dat 1 kilo weegt en gezien hebben hoe groot een kubieke meter is. Die lijst is nog met veel meer aan te vullen en dit wordt dan ook een thuisopdracht waar de cursisten samen met hun collega's over na gaan denken. Bovendien worden ze uitgenodigd om in hun eigen klas meteen te beginnen met de opbouw van maatkennis. Aan het begin van de volgende cursusbijeenkomst zullen er ongetwijfeld veel tips en lesideeën voor de opbouw van maatkennis over tafel gaan. 'Wat is het toch ontzettend belangrijk om steeds weer kritisch naar je eigen onderwijs te kijken.' overweegt een cursiste aan het eind van de bijeenkomst.

Tenslotte

Deze blik in de try-out-keuken van de NCRC-module 'Meisjes-Jongens' laat zien dat bepaalde aspecten van het reken-en wiskundeonderwijs, zowel didactisch als organisatorisch verbeterd kunnen worden. De opbouw van maatkennis is maar één onderdeel. Het cursusprogramma bevat ook onderwerpen als: flexibel rekenen, schatten, meten en meetkunde, het oplossen van niet-typische opgaven, het houden van interactieve leergesprekken, het creëren van een veilig klassenklimaat, enzovoorts. Als het onderwijs op deze punten verbeterd zou worden, profiteren de jongens daar natuurlijk ook van, dus zullen verschillen tussen meisjes en jongens waarschijnlijk nooit helemaal verdwijnen, maar als beide groepen er werkelijk beter van worden, is er een mooi doel bereikt. In september 2000 wordt de voorscholing van deze module voor Pabo-docenten en schoolbegeleiders gehouden. Daarna zal de module 'Meisjes-Jongens' in het hele land voor geïnteresseerde rekencordinatoren van start gaan.

De auteurs van dit artikel zijn werkzaam bij het Freudenthal Instituut als ontwikkelaars van de NCRC-module 'Meisjes-Jongens'.

Voor nadere informatie over de cursus voor rekencoördinatoren kunt u de website bezoeken: www.fi.uu.nl/ncrc

Literatuur
1. M. van den Heuvel-Panhuizen en H.J. Vermeer (1999). Verschillen tussen meisjes en jongens bij het vak rekenen-wiskunde op de basisschool. Eindrapport MOOJ-onderzoek. Utrecht: CD-ß Press/Freudenthal Instituut.