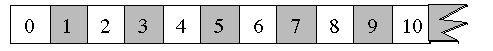
Durante los pasados tres años, varias escuelas puertorriqueñas han empleado en forma experimental los materiales de Las matemáticas en contexto: un currículo coherente para los grados 5-8 (MeC). Estos materiales en sus aspectos matemáticos fueron desarrollados por el Instituto Freudenthal de la Universidad de Utrecht en Holanda y revisados para adecuarlos a la realidad educativa norteamericana por el NCRMSE (National Center for Research in Mathematical Sciences Education) en la Universidad de Wisconsin, Madison. Los materiales han sido traducidos al castellano y adaptados parcialmente a las circunstancias peculiares de la educación matemática puertorriqueña por el CRAIM (Centros Regionales de Adiestramiento en Investigación Matemática) en la Universidad de Puerto Rico en Río Piedras. El material didactico de las MeC se desarrolló con la idea de confeccionar un currículo completo par los grados indicados, en total armonía con los lineamientos propuestos en el documento, Estándares de Currículo y Evaluación para la Educación Matemática del NCTM (National Council of Teachers of Mathematics). Las unidades constituyen lo que a mi juicio es una instrumentación efectiva del método realista de la didactica matemática. Esta filosofía de la enseñanza matemática se fundamenta en un famoso paradigma de Hans Freudenthal, el cual equipara el aprendizaje matemático con la reinvención dirigida de la matemática, es decir, con la reinvención de la matemática por parte de los alumnos bajo la guía de los adultos (maestros) [3, 4, 5]. Este reconocimiento del carácter constructivo de todo conocimiento matemático es uno de efectos normativos en la matemática realista, teniendo el efecto de regir el diseño de todo currículo matemático así como la producción de las unidades didacticas correspondientes. En la matemática realista, la instrumentación del currículo matemático se atempera constantemente a las realidades observadas en las aulas donde se el mismo se pone en práctica. El desarrollo curricular realista es uno autovalidable ya que por su propia naturaleza (y a tenor con el paradigma de Freudenthal), el mismo se ajusta sobre la marcha para que responda adecuadamente a los requisitos cognoscitivos de las poblaciones estudiantiles que emplean el currículo. Como es de esperarse, el punto de vista constructivista implícito en la idea de la reinvención dirigida de Freudenthal tiene profundas consecuencias metodológicas en la educación matemática realista. Por ejemplo, la didactica realista reconoce que hay una gran lección que aprender de la historia del desarrollo de las ideas matemáticas [9]. También reconoce que en la enseñanza contextual característica de la educación matemática realista es necesario emplear todo tipo de producciones estudiantiles como, por ejemplo, aquellas notaciones transitorias que desarrollan los mismos estudiantes en sus intentos por entender las ideas estudiadas [11]. Tales notaciones, aunque más rústicas y menos depuradas que las notaciones más modernas, resultan muy útiles para el estudio, precisamente por la cercanía que tienen a los contextos primarios de estudio de donde surgen inicialmente las ideas matemáticas. Todas estas ideas han sido discutidas ampliamente en otros lugares, de manera que no abundaré más en ellas. Me dedicaré, a cambio, a describir una posible instrumentación del método realista en el estudio del álgebra.
En las unidades de las MeC, desde los grados más primarios, el camino al álgebra se pavimenta explotando patrones de todo tipo. Las tablas y los arreglos numéricos dan origen a todo tipo de consideraciones algebráicas. Consideremos la siguiente cinta "interminable":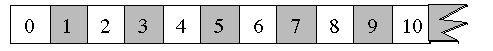
Como puede observarse, la cinta parece estar "rasgada" en su extremo derecho. Consideremos también la segunda cinta que se presenta a continuación: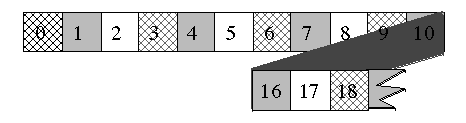
Nótese que la segunda cinta también parece rasgada en su extremo derecho y que hay varias entradas numéricas que aparecen ocultas a la vista en la parte del doblez. Esta introducción de las sucesiones como cintas infinitas ofrece una multitud de posibilidades didacticas. Por ejemplo, si observamos los números en los cuadrados blancos de la primera cinta, podemos generar la siguiente tabla de patrones: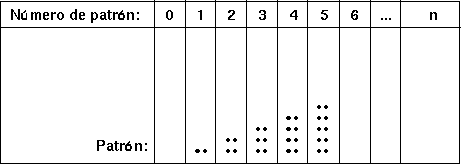
En la entrada correspondiente la tabla indica el número de patrón "genérico" n para que los estudiantes conjeturen la fórmula correspondiente. Los niños más jóvenes se exponen a todo tipo de patrones numéricos. 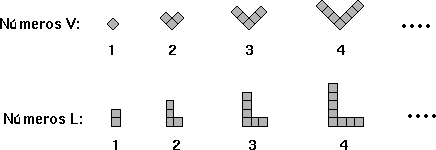
Números triangulares: 
Además, desde temprano los estudiantes descubren patrones interesantes entre algunos de los números geométricos indicados: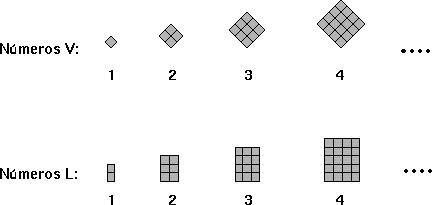
Es interesante observar que muchas "equivalencias" del álgebra más abstracta surgen con naturalidad al estudiar patrones numéricos y al emplear métodos combinatorios para contar los elementos constituyentes de tales patrones. Por ejemplo, supongamos que en una fábrica de vigas de metal se producen vigas que describen patrones triangulares como los que se muestran en los diseños siguientes:
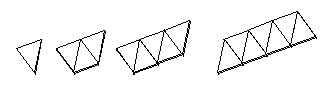
Si preparamos una tabla para organizar la información dada, podríamos obtener una como la que se muestra en la página próxima. Los estudiantes que llenan la "columna de n" lo pueden hacer de varias maneras. Ellos podrían, por ejemplo, "conjeturar" o "adivinar" la fórmula a base de la información de la tabla, es decir, basándose en los posibles patrones numéricos que la tabla pudiese delatar. Sin embargo, otros estudiantes justifican su entrada en la columna correspondiente a n a base de estrategias de conteo.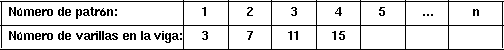
A continuación se presentan varias estrategias de conteo con las fórmulas que "corresponden" a cada uno de ellos.
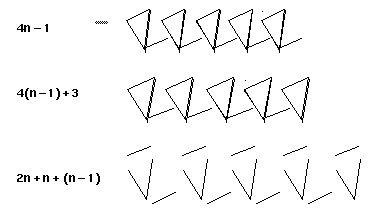
Desde luego, todas las expresiones son equivalentes en el álgebra formal, pero los descubrimientos de tales expresiones por parte del estudiante valiéndose de estrategias combinatorias de conteo resultan muy valiosos ya que constituyen un apresto para el estudio de temas más formales del álgebra.
Otra ilustración. Consideremos el siguiente patrón: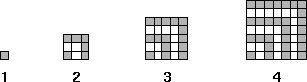
Consideremos la siguiente tabla (incompleta) con filas de diferencias finitas: 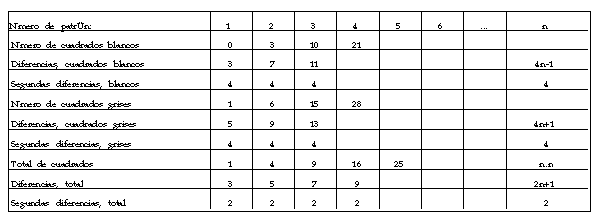
Tablas como esta sirven para propiciar discusiones muy interesantes. Primeramente, obsérvese que todas las segundas diferencias son constantes. Tales diferencias provienen entonces de progresiones aritméticas, las cuales pueden determinarse a partir de las diferencias correspondientes. Siendo entonces la sucesión de primeras diferencias una progresión aritmética, se aprecia que las sucesiones de losas blancas, grises y el total de losas son sucesiones que se obtienen como sumas de progresiones aritméticas. Si notamos que los patrones admiten una redistribución de sus cuadrados para formar un patrón equivalente, entonces es más fácil completar las entradas restantes de las tablas.
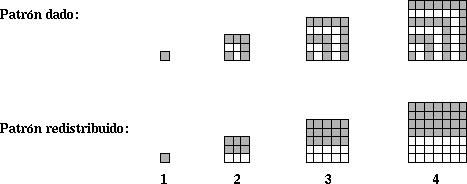
El lector podrá apreciar el valor didactico del siguiente patrón. 
Si se completa una tabla como se hizo para el ejemplo anterior, tenemos: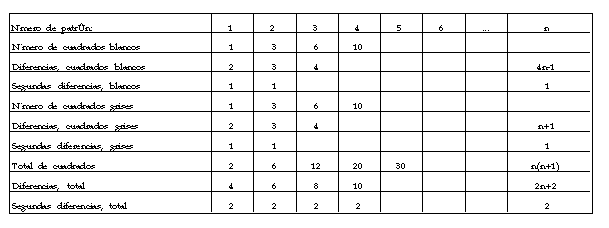
Las entradas que restan por llenar se pueden completar de inmediato si se observa que los cuadrados grises y los blancos son iguales en cantidad, siendo ésta la mitad del total de cuadrados. Como el número de cuadrados grises del patrón n es claramente igual 1+2+...+n, vemos que 1+2+...+n = n(n+1)/2. Desde luego, tal resultado también puede explicarse combinatoriamente; observe la siguiente figura: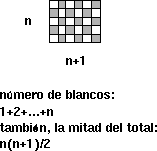
Evidentemente, el escenario descrito es muy rico para la introducción de ideas algebráicas que llevan al estudio más formal del álgebra. La matematización vertical [8, 11] que se debe desarrollar para alcanzar un conocimiento más formal hacia el final de la escuela superior (típicamente estudiantes de 17 años) ciertamente requiere la discusión del principio de inducción matemática. Además, los aspectos más formales pueden llevar a la discusión de temas de las ecuaciones de diferencias. La discusión de las diferencias finitas resulta muy interesante. Por ejemplo, las diferencias finitas constantes son diferencias finitas de progresiones aritméticas. La sucesión de diferencias finitas de una progresión geométrica es otra progresión geométrica, y una sucesión de diferencias finitas es una progresión geométrica si la sucesión original también lo es. Finalmente, la discusión presentada muestra que el "teorema fundamental" del cálculo de diferencias finitas se puede deducir fácilmente de los escenarios de exploración descritos. Este contexto hace posible el desarrollo de métodos para sumar los términos de varios tipos de sucesiones. En tal discusión se introduce naturalmente el triángulo de Pascal, útil para la búsqueda de sucesiones cuyas diferencias finitas sean sucesiones dadas de antemano. Una vez determinadas tales sucesiones, los términos de la sucesión dada se podrán sumar en forma cerrada sin mayor dificultad.
REFERENCIAS
[1] Assessment Standards for School Mathematics, National Council of Teachers of Mathematics, Working Draft, October 1993
[2] Curriculum and Evaluation Standards for School Mathematics, National Council of Teachers of Mathematics, 1989
[3] de Lange Jzn, J. 1987. Vakgroep Onderzoek Wiskunde Onderwijs en Onderwijscomputercentrum, Rijksuniversiteit Utrecht
[4] Freudenthal, H. 1973. Mathematics as an Educational Task. Dordrecht: Reidel
[5 ] Freudenthal, H. 1983. Didactical Phenomenology of Mathematics Structures. Dordrecht: Reidel
[6] Freudenthal, H. 1991. Revisiting Mathematics Education. Dordrecht: Kluwer
[7] Gravemeijer, K.1994. Development of Realistic Mathematics Education Center for Science and Mathematics Education, Freudenthal Institute Group on Mathematics Education, Utrecht
[8] Kindt, M. 1993. Enfoque realista de la educación matemática, Aspectos Didacticos de las Matemáticas. 4. Instituto de Ciencias de la Educación, Universidad de Zaragoza
[9] Streefland, L. 1991. Fractions in Realistic Mathematics Education. A paradigm of developmental research. Dordrecht: Kluwer Academic Publishers
[10] Treffers, A.E. 1987. Three Dimensional. A Model of Goal and Theory Description in Mathematics Education Dordrecht: Kluwer
[11] Treffers, A. 1991. Realistic Mathematics Education in The Netherlands 1980-1990, in: Streefland, L. (ed.),1991. Realistic Mathematics Education in Primary School , Research Group on Mathematics Education, Center for Science and Mathematics Education, Utrecht University, The Netherlands
Generated with CERN WebMaker