Oplossen van vergelijkingen
Voor het oplossen van vergelijkingen zijn vele modellen en strategieen voor handen.
Voordat leerlingen vergelijkingen gaan oplossen, is het nuttig dat ze ontdekken hoe vergelijkingen (en expressies) ontstaan.
Er is een serie applets ontwikkeld die kunnen helpen bij het ontwikkelen van het inzicht in wat vergelijkingen zijn en bij het oefenen van vaardigheden in het oplossen van vergelijkingen.

Hieronder wordt een kort overzicht gegeven, waarbij de applets geordend zijn van informeel naar formeler. 		  Met het onderwerp vergelijkingen kan al vroeg (klas 1) worden begonnen.

Hieronder een toelichting per applet. 		 
Geometrische Algebra 1D


Expressies (formules) maken die bij een pijl horen. 		  Het applet Geometrische Algebra 1D kan goed gebruikt worden in de verkennende fase om een beeld te krijgen van wat een vergelijking is.
Getalen en variabelen worden weergegeven door middel van pijlen met vaste en variabele lengtes. Met deze pijlen kunnen expressies worden gemaakt. Door de lengte van ene gebruikt variabele aan te passen kunnen vergelijkingen worden opgelost.

voorbeeld, voor welke waarde van x heeft de pijl een lengte van 8 		 
Waarmakers


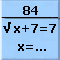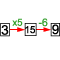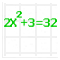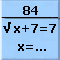
allerlei soorten vergelijkingen oplossen
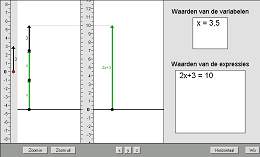
een oefenapplet 		  Het applet waarmakers bevat een hele serie vergelijkingen (van verschillende soort en verschillende moeilijkheidsgraad) die moeten worden opgelost. Het applet geeft feedback door aan te geven of een vergelijking juist is opgelost of niet.

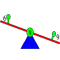
Vergelijkingen worden hier gepresenteerd als puzzels waarin je een onkende waarde moet zoeken, zonder dat er een kant en klare strategie of algoritme wordt aangeboden. Doordat de oplossingen gehele getallen zijn zijn er ook allerlei eigen strategieen mogelijk, zoals: goed kijken naar de formule, handig proberen en controleren.
Deze eigen strategieen bevatten vaak al elementen van bijvoorbeeld de bordjesmethode of de terugrekenmethode en vormen daarmee een goede voorbereiding op het oplossen met formele strategieen. 		 
Vergelijkingen oplossen met de bordjesmethode


een vergelijking in stukjes oplossen 		  Het applet bordjesmethode
biedt een strategie om een vergelijking op te lossen door delen van de vergelijking af te dekken. Je kunt een deel van de vergelijking selecteren en de vergelijking eerst voor dat deel op te lossen. Deze substitutie-strategie werkt ook in niet-lineaire situaties. 		 
Algebra Pijlen


om expressies en formules mee te maken
  Met het applet Algebra Pijlen kunnen rekenstappen (bewerkingen) aan elkaar worden geschakeld. Door in plaats van getallen variabelen (letters, woorden) als invoer te gebruiken, ontstaan formules.
Van de formules kunnen grafieken worden getekend en tabellen worden gemaakt. De grafieken en tabellen kunnen worden gebruikt om vergelijkingen op te lossen.

Een andere strategie om met dit applet vergelijkingen op te lossen is door de omgekeerde pijlenketting te maken (uitvoer wordt invoer). 		 
Vergelijkingen oplossen met de weegschaal

het weegschaalmodel om lineaire vergelijkingen op te lossen 		 
met het weegschaalmodel zijn vergelijkingen op te lossen door aan beide kanten van de vergelijking hetzelfde te doen. Met dit applet geven leerlingen aan welke bewerking (aan beide kanten) op de vergelijking moet worden toegepast. Het applet doet vervolgens het rekenwerk. 		 
Vergelijkingen oplossen met de weegschaal, spelvariant


lineaire vergelijkingen oplossen met puntentelling en meer eigen inbreng 		  Het applet weegschaalmodel, spelvariant is in principe hetzelfde als het "gewone" weegschaal applet.
Met deze variant van het weegschaalapplet moeten leerlingen zelf intypen wat het resultaat is van de bewerking die ze op de vergelijking willen toepassen. Ze kunnen hulp opvragen (het applet doet dan het rekenwerk), maar dat kost punten. 		 
vergelijkingen oplossen, kwadratisch en meer


een aantal methoden bij elkaar voor het oplossen van verschillende soorten vergelijkingen.
(Ook kwadratisch) 		  Het het applet vergelijkingen oplossen, kwadratisch en meer zijn ook andere dan lineaire vergelijkingen op te lossen.
Met het applet kun je ook ontbinden (buiten haakjes brengen). De mogelijkheden zijn verder hetzelfde als die van de spelvariant van het lineaire weegschaal-applet. 		 
In het kader van het WELP-project is leerlingenmateriaal ontwikkeld rond algebra met applets voor klassen 2 en 3 van Havo/VWO. Dit materiaal wordt momenteel gereviseerd en zal in het voorjaar op de WisWeb+site verschijnen.
© Copyright 2004 - Freudenthal instituut - WisWeb last modified: 17-12-2003