Periodiciteit

Mathematisch Instituut, Universiteit Leiden

Vrijdag 15.45-16.45 uur

Periodiciteit is een fundamenteel begrip in de wiskunde (en de natuurkunde en de sterrenkunde). Het doet zich voor bij rijen en bij functies. In het voorgestelde profiel Natuur en Techniek voor vwo wordt expliciet aandacht besteed aan periodieke bewegingen zoals cardioïdes en cycloïdes. In deze voordracht gaat het vooral om periodieke rijen, met materiaal dat zich leent voor behandeling in de klas.

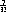1. Periodieke ontwikkelingen.
De decimale ontwikkeling van een breuk is eindig (bijv. van ) of periodiek (bijv. van 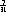). Welke ontwikkelingen breken af? Wat kan je zeggen over de periode als zij niet afbreekt? Is er verband tussen periodes van breuken met dezelfde noemer?

2. Resten van de veelvouden van een getal.
De resten van de veelvouden van een breuk zijn periodiek. Wat gebeurt er met de resten bij een irrationaal getal? Een interpretatie is dat een wiel eenparig ronddraait en de plaats waar een punt op het wiel zich bevindt elke seconde wordt opgetekend.

3. Dubbele periodiciteit.
Een periode heet minimaal als zij geen veelvoud is van een kleinere periode. Kan een rij (of reële functie) twee minimale periodes hebben? Niet als de rij oneindig lang is (resp. de functie continu is). Hoe lang kan een dubbel-periodieke rij worden? Hoe ziet een dubbel-periodieke functie eruit?

emeritus-hoogleraar, Technische Universiteit Delf

Zaterdag 9.00-9.45 uur

De rij van Fibonacci (geboren in 1175) is gedefinieerd door de beginvoorwaarden U0 = 0, U1 = 1 en de recurrente relatie Un+2 = Un+1 + Un (n = 0. 1, ...).
De rij bezit vele fraaie eigenschappen. Een aantal ervan kan worden afgeleid uit een formule die Un rechtstreeks uitdrukt in n. Het quotiënt van twee opeenvolgende elementen benadert (met stijgende n steeds nauwkeuriger) het getal 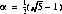, dat een rol speelt in de meetkunde bij de theorie van de regelmatige tienhoek.
De rij heeft ook interessante getaltheoretische eigenschappen. De resten modulo een natuurlijk getal m van de elementen Un vormen een periodiek patroon. Redenerend van daaruit heeft men in de jaren vijftig de rij (en nadien een aantal generalisaties ervan) gebruikt voor het maken van kunstmatige aselecte getallenrijen (pseudorandom numbers), dat is het imiteren van ruis.
Ook op ander gebied heeft de rij toepassingen. In de natuur ontmoet men veel lengten met quotiënt .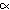

Gaat men uit van iets andere beginvoorwaarden, namelijk V0 = 1, V1 = 2 maar wel met dezelfde recurrente relatie, dan ontstaat de geassocieerde rij van Fibonacci die via een ontdekking van E. Lucas (ruim een eeuw geleden) een methode biedt om onder de getallen Ms = 2s - 1 (van Mersenne, 1588-1648) priemgetallen op te sporen. Het zijn de recordhouders onder de thans bekende priemgetallen; zo af en toe leest men in de krant dat een volgende (voorlopige!) recordhouder is gevonden.

Deze lezing sluit aan op de workshop van A.W. Boon (zie Docentenworkshops).

Spelen met spiegelingen

Faculteit WINS, Universiteit van Amsterdam

Zaterdag 10.00-10.45 uur

Lijnspiegelingen kun je opvatten als de bouwstenen van de bewegingsgroep van het Euclidische vlak: elke beweging kan verkregen worden als een opeenvolging van lijnspiegelingen. Zo is bijvoorbeeld het effect van de samenstelling van twee lijnspiegelingen in onderling loodrechte spiegelassen hetzelfde als dat van een draaiing om het snijpunt over 180 graden. Met andere woorden, het is de puntspiegeling in het snijpunt. Bij elke lijn hoort precies een lijnspiegeling en bij elk punt hoort precies een puntspiegeling. Punten en lijnen uit de vlakke meetkunde corresponderen zo met de involutorische elementen van de Euclidische bewegingsgroep, dat wil zeggen de elementen waarvan het kwadraat het eenheidselement in de groep, de identieke afbeelding, is. Het verrassende is dat je op deze

manier allerlei meetkundige stellingen kunt vertalen in groepentheoretische termen, waarna je ze helemaal algebraïsch kunt bewijzen.