The depth of the plane

Aad Goddijn
University of Utrecht

This article was previously published in the `Nieuwe Wiskrant', a Dutch journal on innovations in mathematics education. While the introduction has been adapted for ICME8, nothing else has been altered starting from the section entitled "Back to Euclid?"

The development research described in this article is part of an innovative mathematics project for the final years of secondary education. Many of the students for whom this project is intended will continue further at the university level with one of the hard sciences, or engineering. Until now, the Freudenthal Institute has had little influence on the mathematics curriculum followed by such advanced students before they enter the university. Where future classes of this target group are concerned, one may expect that they will have used mathematics materials in the earlier years of secondary education that have been tailored to the `realistic' concept advocated by the Freudenthal Institute.

In this concept of mathematics education, geometry is seen at this stage as a broadly intuitive spatial orientation, with the focus on application. `Space' often means `real' space. In this approach to geometry, much of the curriculum involves spatial geometry, where a great deal of reasoning is necessary, albeit seldom in a more formalized mode. Clearly, with the focus group described above, attention should be devoted to more proof-oriented aspects of mathematics. This is, naturally, also true where the project deals with the calculus section of the curriculum. But in geometry as well - and particularly in traditional Plane Geometry - there are terrific opportunities to explicitly address the systematic construction of a subject area. This project - known in The Netherlands by its acronym `PROFI' - involves piloting a newly developed curriculum in a small number of experimental schools. The experiences gained are then reported upon in publications and used to make an improved version of the developed unit. All of these experiences and results are available for teachers, educators and, naturally, commercial publishers. One comment on the Dutch situation: virtually only the older generation of mathematics teachers (those who are at least about 45 years old) are familiar with traditional plane geometry from their own schooling.

Back to Euclid?

First of all, let us look back more than two thousand years, to Euclid's Elements. Virtually everything known about mathematics at that time was presented in the Elements in the form of a systematic construct made up, according to the rules of logic, of a number of basic assumptions, namely, the axioms. During the Dutch `National Mathematics Days', in February, 1996, Professor S. J. Doorman argued the importance of this approach, and recounted how it occurred at a time when one had to use argumentation to prove one's point. At the time, one might also say, when the idea of `democracy' arose. If argumentation is important, then arguments must be testable, and judged according to their value. A certain school of philosophy, namely, that of the sophists, is important here. The sophists took an extremely critical look at the entire process of reasoning by, for instance, inventing all sorts of argumentations that appear perfectly logical, but that lead to bizarre conclusions: the paradoxes. So that mathematics would not become vulnerable in a similar fashion, the system of the Elements as we know it was developed. Doorman pointed out that Euclid's methods were also of enormous importance outside of mathematics, in such diverse areas as law, theology, musicology and the other exact sciences.

What we are dealing with here, in short, is one of the roots of western civilization. Doorman mentioned three additional goals of this method, each of which I will describe and provide with brief comments.

Firstly: making knowledge memorable. Since we have moved from an oral tradition to the art of printing and are heading towards a digital world, one would expect this argument to have become less significant. Nevertheless, systematically organized knowledge is easier to remember than unorganized knowledge - it's as simple as that. What is certainly still important for us is the link between the systematics of the subject matter and the teaching methods. Throughout these two thousand years since Euclid, the instructional theory of geometry education has virtually coincided with the mathematical construction of the geometrical system. In other words, where the organization of subject matter and style are concerned, Euclid continued to determine which path would be followed. It was not until this century, in fact, that any divergence from this path took place - as in fact also occurs in the Profi project. (We will deal with this in detail shortly.)

Secondly, Doorman mentioned the systematic production of knowledge. The hope was that, if the reasoning process could be mapped precisely, one would then be able to generate new knowledge - for instance, a new theorem - in a dumb, almost mechanical way. In actuality, this only became important in our century, and then only to a limited extent. Here, too, let us interject a note of instructional theory: while we all would like our students to be able to manage the subject matter independently, opinions differ - to put it mildly - with regard to the appropriateness of traditional plane geometry. Wasn't this the area of mathematics where, as a student, you used to stare at the wonderful construction line - the one you never managed to find yourself? In short, we must do something about how we teach our students to find argumentations, proofs, and suchlike. Otherwise there will be trouble.

Thirdly, and perhaps most importantly, is the certainty of knowledge. If your points of departure are true and your reasoning is correct, then your result must be true, mustn't it? In actuality, this `truth' of the points of departure and the making of a `correct' choice have been topics of discussion throughout the centuries since Euclid. The self-evidence of axioms, for instance, has had to be abandoned due to the discovery of a logically correct geometrical system that severely clashes with that of Euclid. For this reason, at the beginning of this century, geometry became (or declined into) a purely logical system, separated from `geometrical objects' and certainly divorced from any kind of reality. Certainty was regarded as logical certainty, and intuition was no longer allowed to play any role at all. Mathematics, however, is a subject with a living history in which the emphasis continually varies. Roughly speaking, one could state that interest in the geometrical object itself is again increasing, and that research into the logical foundations of geometry is no longer the primary center of attention.

At the forefront now is the interest in the link between what used to be separated areas of geometry. It should not be surprising that this is exactly the focus with this target group of students: their geometric intuition needs to be developed, but also their logically based criticism of `that which is mere appearance'. Every student may be permitted to become a bit of a sophist - there's no harm in that. This introduction and glance backwards is, of course, implicitly rather idealistic. But a design group needs to be idealistic, as well as somewhat skeptical and also able to put things in perspective. At any rate, for the following reasons, the present situation does seem to be more favorable than ever in terms of achieving high ideals:

the students now have a broader intuitive foundation in geometry, thanks to the current curriculum that is being used in the earlier years of secondary school;
the students in this target group are somewhat older than those students who used to have to juggle the various properties of congruencies, angles, arcs and missing construction lines; they are older and, especially, more mature in the sense that they are able to deal with mathematics in a more reflective fashion.

The following are a number of essential questions with regard to the geometry in the profi-project:

does this mean that geometry at this level is again going to be taught according to the book of Euclid - just as this both succeeded and failed a number of times in the past?
are there no new - modern - topics?
what is the general organization of the topics?
how does it all work out in the classroom?

This article will provide examples that deal with these questions indirectly; in the summary at the end of the article the questions will be answered more explicitly. First, however, a brief description of the subject matter itself.

The first half

At this moment, namely, March, 1996, the first half of the 60 hours of the new curriculum of Plane Geometry has been covered in the experimental classes. A unit, entitled Distances, Boundaries and Area classification was used. Its chapter titles are:

Chapter 1: Voronoi diagrams
Chapter 2: Iso distance lines
Chapter 3: Convexity

Voronoi diagrams have already been discussed in detail in the Nieuwe Wiskrant (Goddijn, 1995). I will not deal with them any further here, in part to avoid creating the impression that Voronoi diagrams are THE topic of profi-geometry. In the experimental design, Voronoi diagrams proved to be a good introduction to plane geometry; they also provided the opportunity for a noteworthy modern application of this geometry. But they are not an end in themselves, as was already obvious after the previous section of this article.
Iso distance lines play the same role: they are a topic of geometry in which traditional plane geometry can function nicely. See, in this regard, the article `Plane Geometry: is it worthwhile for Mathematics B?' (Kindt, 1995). See, too, the article by J. van Maanen, `On the division of alluvial land; a seventh-grade class project' (Van Maanen, 1984). In this project, bisectors and perpendicular bisectors were dealt with in a historical context.
Mathematically, it all has to do with areas in the Euclidean plane and with special lines that surround the areas. These lines indicate the points that are located at a fixed distance from the area.
Convexity is a property of figures that one does not find in Euclid (but does, by the way, in Archimedes). This property is introduced in a natural fashion in the first two chapters of the text unit. It is a property of figures in general, and not, therefore, exclusively a property of figures constructed from circle or straight line segments. For this reason, it is also belongs to more modern mathematics, particularly because the link with calculus is so strong here. A broadening of the concept of `tangent' (namely, in the sense of `support line') plays an important role in this chapter. The few examples included at the end of this article should make it clear that, with respect to this concept, rather refined reasoning is possible, useful and necessary. The present article will not go into the details of the unit and its accompanying computer program. A revised version of the unit will be available in the fall of 1996.

Test problem on iso distance lines

The first two examples show answers to a test problem from Chapter 2. The problem was designed by Ramiro Wanga of the Calscollege, one of the experimental schools involved in the profi-project.

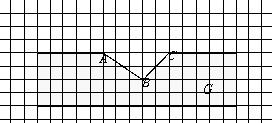
This figure shows an area G, and the points A, B and C. (Each square is 1cm by 1cm.)

a. Draw the iso distance lines at 1, 4, and 8 cm from G (where possible)
The iso distance lines have a kink in them
Three types of kinks are possible, depending on the distance from the area G, namely: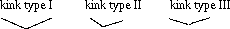

b. Determine the spot where the transition from kink type I to kink type II occurs.

c. Also determine the spot where the transition from kink type II to kink type III occurs.

d. The kink points of type I lie along the bisector of the angle ABC. The type III kinks also lie along a (special) line. Which line is this?

For the sake of the reader's orientation, more iso distance lines than were requested have been drawn in figure 1 below. The set of kinks can be clearly seen. The transitions between the kink types are found at the intersections of the added lines (perpendiculars to AB in A and to BC in C). Kink type III can be found in the top section of the perpendicular bisector of AC, kink type I on the bisector coming from B, where it has not yet passed the perpendicular to BC coming from C, and kink type II on the segment in between. This segment is not a segment of straight line, as will be seen later.

fig. 1: Iso distance lines near the indentation

The following figure is Kaspar's solution; again, only the relevant detail near the indentation (see figure 2).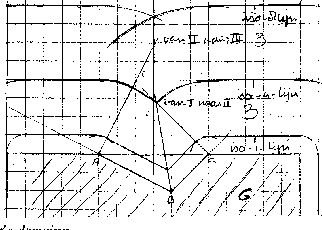

fig. 2: Kaspar's drawing

Everything of importance is shown in this drawing: the correct arcs and line segments, the bisector coming from B and the perpendicular bisector of AC. Kaspar had clearly mastered these simple elements of plane geometry sufficiently to be able to independently solve a problem that had not yet been presented in this form. Although iso distance lines had, of course, already been dealt with, this was definitely not true of the types of kinks in this context. Personally, I would have liked to have seen the answer to a problem that was not included on the test, namely, whether the iso-4-line marks the exact transition from type I to type II. With some effort, the answer - no - can be found in figure 1. Kaspar's work shows that this test problem, as expected, was not too difficult. For the purposes of this article, however, it will be more instructive to look at an incorrect solution. In Bart's drawing, the iso-4-line has no kink at all.

He sketchily added something to the precisely determined arcs and lines.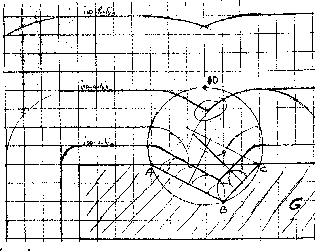

fig. 3: Bart's drawing

The consistency in Kaspar's work - which is entirely in the Euclidean style - has yet to be achieved by Bart. And yet, other interesting elements can be found in Bart's drawing, for instance: all those little arcs whose midpoint lies on the edge of G, and the circle through A, B and C, that he evidently found by intersecting the perpendicular bisector of AB and BC. All of this had been dealt with in the first two chapters of the project material. The small circles whose radius is 1 together determine a surrounding line - the iso-1-line. Here, Bart carefully put into practice what he had learned but did not - at least in the case of the line at distance 4 - apply this knowledge consistently; and the ability to consistently apply information is a precondition for being able to understand and build a mathematically correct proof. This section has devoted some attention to bisectors and perpendicular bisectors. These are loci: sets of points having a specific property.

In the second part of this unit of Plane Geometry - now being developed - this concept is developed further, and explicit attention is paid to the general technique of finding proofs that is linked to it. The first two chapters of the second part of this unit provide an introduction to this technique of finding proofs.

In search of the foundation

Anyone who has looked at Euclid's Elements knows the structure of the book: an entire system has been constructed from five axioms. Only the axioms are assumed to be true initially. But have we made a clear enough agreement with our students about just what our basic truths are? We did not, in fact, do so in the unit described here. And we had our reasons for not doing so too quickly.

In the first place, our standpoint is that, while an entirely deductive construction based on axioms is mathematically correct, educationally speaking it is certainly not the best approach. If you truly wish to work deductively, you are forced to start with the most difficult part of geometric reasoning; in other words, you must reason from very little information towards something that you intuitively know to be true already, but are not supposed to accept until you have done some highly specialized thinking. It is interesting to note that Euclid himself made a mistake in his very first proof by making an assumption that could not actually be based on one of his axioms. Moreover, this kind of `basic reasoning' does not immediately produce a wealth of figures and interesting relations. For this reason, we began, as it were, `in the middle' of the system. That provided, among other things, valuable conflicts for the students.

A second reason to avoid determining such things as axioms too quickly is that the students must have the opportunity to participate in this determination process themselves. The following example pertains to this. In the first chapter, triangle inequality was introduced as follows:

The figure below shows three points and their connecting lines.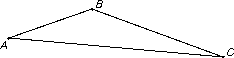

a. Write d(A, C) on the correct side in the figure.

b. Do you agree with this inequality: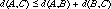

c. Translate this inequality into a Dutch sentence. What does this inequality mean?

It has been pointed out to me that, in mathematics, one does not ask: `Do you agree?' This was, naturally, a bit provocative. Its effect, however, was not felt at that moment but, rather, in a lesson a few weeks later. By that time, a good deal of discussion had taken place on reasoning. "That stuff about the triangle inequality", said one student. "That's kind of vague. Why should we assume that?" "Well, we have to start somewhere", I replied. "And if I had chosen something from which you could derive the triangle inequality, you would still have said, `why should we assume that' ". The conversation went back and forth like this for a while, until I thought, "and why not, anyway?" So I said, "What would you like to assume as a basis - something that you know for certain?" "The Pythagorean Theorem, that's definitely been proved", replied the student immediately. "OK", I said, "then try to derive the triangle inequality from The Pythagorean Theorem!" Ten minutes later I was asked to look at the following figure, along with the accompanying proof: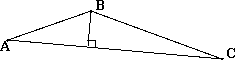

Whether or not one can indeed prove The Pythagorean Theorem without making use of triangle inequality - that is a question I will pass over. I offer this example purely in order to show that this conversation with the student could take place thanks to the fact that the points of departure had not been entirely fixed beforehand and were still open for discussion. This student accepted the challenge to search for the underlying foundation of geometry himself. He followed the logical path towards the bottom of the pyramid.
We are in good company here. With respect to reasoning, Aristotle says that the search for the points of departure - the downward search in the deductive pyramid - is at least as important as the deduction itself. The Elements is the end result of this kind of a thought process and does not reveal the search process itself. But it is precisely this process that we do want the students to experience themselves.

In search of the boundary

In the previous section I introduced a student who dug below the surface of what had been presented. Now we meet another student, Karin, who worked from the opposite direction: she tried to deduce much more than would seem possible. In order to see things in the correct perspective, this next classroom report begins just before the conversation with Karin.

During the work on Chapter 2, two boys were busy with figure 4. The mistake made by the boys is typical for the problems in this chapter: the basic elements of the problems are often simple in themselves, but these simple elements are easily applied incorrectly in a broader situation.

After a brief discussion, however, the boys got back on track without much assistance. Suddenly, everything was obvious. Effortlessly, they were able to figure it all out: if the distance is less than 2.5, there will be a straight segment (of a known length). After that, the angle of the kink will become smaller. But it will still be there. The angle of the kink becomes increasingly wide - almost 180xb0 .

This is a fine theorem, and it was independently formulated. It is particularly admirable if one considers that the iso distance lines in many popular articles on this topic are drawn much too smoothly.

fig. 4: The line in bold is not a good iso distance line!

While we were discussing figure 4, Karin joined us. She waited patiently until we were done, without joining in the discussion. Her questions pertained to figure 5. This figure, too, involves iso distance lines that may have kinks.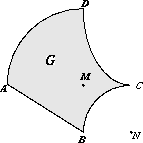

fig. 5: A trickier area

The text states the following:

The frontier of the area G consists of a straight section and three curved sections. AD is a quarter-circle around M, BC is a quarter-circle around N.

a. Draw the iso distance line at 1 cm around G. Where necessary, use circles around points of the frontier of G.

b. Also draw the iso distance line at 2 cm and at 3 cm off the coast of BC.

c. Above a certain value for d, the iso distance line will show a kink. How large is this distance d?

Karin was well aware that with short distances - no farther than N - the arc BC would be responsible for a smooth circle segment, and that, with greater distances, it would cause a kink in the iso distance lines. But she wanted to know what would happen with the curved section CD.

We started sliding different sized coins around the table, and imagined how bicycle wheels would rotate as well. This is the usual technique of rotating circles and their centers. While no kinks seemed to appear with the small coins, they did emerge with the bicycle wheels. They tilted around D and bumped into the angle C. In Karin's opinion, there had to be a radius where the kinks began to appear; they would be present at greater values but not at lesser ones. She wanted, as with BC, to find this boundary. At that moment I realized that Karin should go study mathematics and take a course in differential geometry. After four years of study, she would have it figured out. My answer was that it was possible to find the exact spot, but that it would be difficult to do this exactly. End of discussion? No way! A little while later, she came up with a piece of the solution. That is to say, she did something that led to deeper insight, namely, she showed how the boundary could be found (see figure 6). Karin had found the tangent circle in D that passes through C. In her drawing, T is therefore a point on the iso distance line that has - as Karin put it - the last kink; (in other words, if you take a shorter distance there will no longer be a kink). At this level of schooling, one no longer asks for constructional details for finding point T. The colliding circle has been drawn and we may assume that the iso distance line indeed runs more or less as is indicated at T.

"If the distance is shorter, then there are no kinks", said Karin.

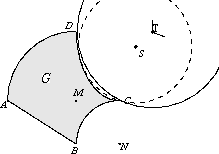
fig. 6: Interim answer: T is the first kink

"Hmm", I replied. "Will this really be the case if you take somewhat shorter distances?" I asked, making a brief sketch. Karin believed that this would be possible, but I do not. In my opinion, the direction of the iso distance lines will continuously depend on the location and the foot of the connecting line to G, so, consequently, if there are two feet there will be a kink. But my scribbles did not convince her. What would happen if we made the circle at D a little smaller? Then it could slide downwards a bit, but it would still bump into C. (See the dotted circle in figure 6.) I suggested to Karin that she take a look at problem 24, which deals with the same kind of thing. In this problem, an iso distance line is drawn on the inside of the parabola, with the aid of normals on the parabola. (An illustration can be found in the earlier mentioned article, `Calculus in profile' (Drijvers and Kindt, 1995). Karin took my suggestion and, a bit later, showed me her sketch. It was similar to figure 7, and she had drawn in about ten normals. An envelope around the normals was also clearly visible.

fig. 7

"If the iso distance lines go under there", said Karin, "then there are no kinks." By `there' she meant where the normals begin to get in each other's way. The class period ended at that point, but after class the teacher, Paul Thiel, remained at the blackboard with two students. Their discussion, too, concerned the kinks in the iso distance lines, but their question was more specific: what is a kink anyway? Or, seen in the light of Euclid: what is the definition? After a few minutes of discussion, one of the students formulated it as follows: `where it jumps from one to the other'. I drew two intersecting circles on the board.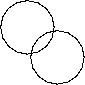 "You mean where you can pass from one circle to the other"? I asked. Yes, that is precisely what he meant. In the examples given, that is exactly what had occurred up to now!

Convexity, support line, tangent

Interesting events involving iso distance lines always occur because of indentations in the area. The third chapter covers areas without indentations. The discussion is on the following definition of the concept of convexity: where all points in the entire area can be connected with straight lines. An essential key in this chapter is the concept of support line. The following is the description and an accompanying problem:

A line l is a support line for an area G if:

G lies entirely in one of the half-planes determined by l
the line l shares at least one point with the frontier of G.

a. Which of the lines l, m, n, o, p and q drawn here are support lines for the area G?

b. Is every support line for the area G a tangent to G?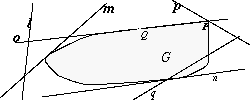

fig. 8

The following now needs to be proved: in a convex area, at least one support line passes through each point on the frontier. Intuitively, this is quite obvious, but it is not so easy to find a proof that works well on this level. Only the definition of convexity may be used in the proof! What is now mathematically necessary is to delve into the subject of `frontier'. But here we purposefully left a gap; we implicitly assumed a clear understanding of `area' - that an area is encompassed by a curved frontier, that the frontier belongs to the area, etc. Anyone who insists that the subject matter contain a complete deductive construction will be horrified by this, of course. But those who believe, as we do, that it is natural when learning mathematics to begin with a problem area and then to reason both towards the origins and the consequences, will find this a terrain with a great deal of potential. Back to the support line. A line is a tangent in a point to a convex area if the support line through that point is the sole possible support line passing through that point. In the example given in figure 8, line o is a tangent in Q, but not in P. The following is the `theorem' that concludes this chapter, including an illustration and sketch of the proof:

Iso distance lines around convex areas have no kinks.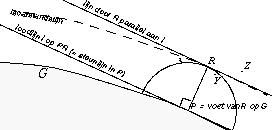

Y lies closer and Z farther from G than the length of PR. The iso distance line through R therefore lies wedged between the circle around P and the straight line through R that is perpendicular to PR. So there can be no kink in the iso distance line at R. The question, `what exactly is a tangent?' was, of course, posed by a student who was working on this chapter. It is a justifiable question, as we now have two tangents: the one from calculus and the one in the convex figures. Actually, that is the provisional answer to the question. In the calculus unit mentioned earlier, the geometrical approach and the approach by way of differentiation were brought together in the example of the circle. Here, the geometric concept of a tangent is stated more broadly: it works for the class of convex figures. This link will be reinforced even more strongly in the revised version.

Summary

To what extent have the essential questions at the end of the section entitled `Back to Euclid?' now been answered?

does this mean that geometry at this level is again going to be taught according to the book of Euclid - just as this both succeeded and failed a number of times in the past?
Yes and no. It is clear that we are attempting to maintain the logical-geometry style of reasoning. But we are forgoing a totally deductive construction. This is how reasoning `towards the bottom' will be able to function.
are there no new - modern - topics?
There are two types of new topics: new subject matter and new applications. Convexity, for instance, is a new terrain in subject matter. It is in itself an important geometric concept, particularly because we do not begin by assuming that the figures are only constructed of `familiar' components. Similarly, with functions, one can speak of x2+1, but of the function f as well. The other new aspect is that certain modern applications of geometry are used, in particular the Voronoi diagrams, iso distance lines and the partitioning of areas.
what is the general organization of the topics?
The organization of part I of plane geometry has already been described. An initial context was chosen in which the geometry of perpendicular bisectors, triangles, angles and arcs appear in a natural manner. In principle, other contexts should also be able to play this role. More important with respect to the organization of the subject matter, however, is the same answer that was given in response to the first question.
how does it all work out in the classroom?
Up until now, very encouragingly. The general impression is that the students have applied a good deal of initiative and have often posed excellent questions. For them as well, the contrast to calculus is considerable; not with respect to effort, nor to the degree of difficulty, but in terms of the kind of reasoning required. And this is exactly the point. Teachers and designers have learned a great deal about what is feasible in this domain. For some topics, more proved feasible than had been expected, and this was then exploited when designing part II and the revised version of part I.

At the end of the 1995/96 school year, the second part of plane geometry will be introduced in the classroom. The working title for this unit is: From Reasoning to Conflict. The chapter titles, and a brief outline of the subject matter are as follows:

Working with what you know (making a list of what you can and can't use in a proof)
Circles, angles, arcs (a traditional topic, but here sharply focused on learning to find a reasoning)
Geometric experimentation (here we use the software program `Cabri'; the concept of locus plays a key role)
And now prove it (using topics from the computer lessons)
Conflict lines and Conic sections (introducing ellipse, parabola and hyperbola through conflict geometry)

In this final chapter, that bit of kink line from figure 1 may come up for discussion: it is, after all, a piece of a parabola!

References

Drijvers, P. en M. Kindt (1995). `Analyse in Profiel', Nieuwe Wiskrant 15 (2) pp. 4-9.

Goddijn, A.J. (1995). `Brand, regen, hunebedden, steunlijnen en kapen', Nieuwe Wiskrant 14 (4) pp. 51-55.

Kindt, M. (1995). `Vlakke Meetkunde, waardevol voor wiskunde B?' Nieuwe Wiskrant 14 (3) pp. 34-39.

Maanen, J. v. (1984). `Over het verdelen van aangeslibd land. Een brugklasproject'. Euclides 60, pp. 161-168.

Reuter, W. en A.J. Goddijn (1995). Afstanden, grenzen en gebiedsindelingen, een meetkunde pakket voor vwo. profi-publicatie. Freudenthal instituut, Utrecht.

ICME8 - WG13 - 02 JUL 96

[Next] [Previous] [Top]

Generated with CERN WebMaker