Similar developmental research to that which has confirmed the usefulness of the `realistic mathematics education' approach, in The Netherlands, the USA, and other countries, needs to be carried out in South Africa under local conditions. Contexts have to be identified locally, which are best suited for classroom mathematization.
Of particular interest for mathematics education is a document of The Department of Arts, Culture, Science and Technology, dated January 1996, (South Africa's Green Paper on Science and Technology Preparing for the 21st Century). It asserts that school level mathematics and science education are particularly important (p 7879), and that research development, technology education, and the promotion of innovation in general, are critical for the country's development and future (see Chapter 3 in particular).
Apartheid policies have left us with a need for capacity building in all spheres, not least in that of mathematics education. For the moment the National Education Department is concentrating on building capacity for the management of schools (Education White Paper2 of February 1996: section 4), which is seen, correctly, as a prerequisite for quality education to take place. Building the capacity of teachers in particular subjects has to receive attention, and will demand much time and hard work before the quality of teaching is satisfactory.
This curriculum document could be improved. The syllabus itself was written according to a paradigm of knowledge and education which is questionable, and inconsistent with the newly expressed aims. Furthermore, there should probably be more variation in future mathematics curricula to accommodate different
needs.
One opportunity which exists for improving the curriculum document, is that each of the nine provinces can formulate their own version of the curriculum (without omitting anything from the core). Thus the topics can be rearranged so as to make more sense didactically, and the core can be annotated with explanations and suggestions. The `final interim' curriculum of the Western Cape Province e.g. is due to be finalized in July this year. In the meantime a series of open workshops were held to allow as much participation as possible. In the Western Cape, I think the process of finalizing the curriculum document is thus more open to participation, and more transparent, than before.
Over the past year, also in the Western Cape, the professional association of mathematics educators, AMESA, has been involved in an in-service education initiative for Junior Secondary Mathematics teachers, in collaboration with the Provincial Education Department. This initiative gave all the junior secondary teachers in the province the opportunity to attend a 16 hour course on the "new approach" involving greater learner participation, and less mechanistic teaching of the subject. The initiative is regarded as successful, and it is hoped it might serve as a valuable pilot study for similar projects in future in other parts of the country. Teachers (about 1000) who participated were given the opportunity to contribute to adapting the interim curriculum, while hopefully gaining insight into the changes in classroom practice now expected of them.
Thus far the background, against which the rest of this paper should be seen...
The `implemented curriculum' is always determined by the interpretations of individual teachers. In South Africa, it is still also partly determined by the intentions of a previous political order.
The `intended curriculum' is designed and/or ratified by the National and Provincial Education Departments. There are however, many variations of the `intended curriculum' in South Africa. Besides the nine official curriculum documents, everyone has their own ideal of what the curriculum should be.
Curriculum change should involve all three these types of curriculum. The official intended curriculum is in the process of being adapted somewhat at the moment, and could still change substantially in the next few years. This depends on the power relationships of those who have strong opinions on what the intended curriculum should be. The implemented curriculum depends as always on teachers themselves, but also on teacher education, including in-service education. To get the implemented curriculum to change is much harder, as it involves persuading most teachers of the need to change. It can also involve a change of behavior for teachers, which might be difficult to effect after years of teaching in certain ways. The very existence of a changed official curriculum is mostly a necessary but not sufficient, condition for change in the classroom. Proof that the attained curriculum improves with a change in implemented curriculum, should help teachers with the process of change.
Nick Taylor and Phillip Methula have this to say about the adoption of an official curriculum document: `Legislation is a move to closure, a delegitimisation of contending interpretations in favor of one approved version...' (Taylor (1993) p 316). This is inevitable.
In the Western Cape Province, the official annotation of the curriculum will have been drafted by a team of people consisting of volunteers with a strong interest in the curriculum, from each of the three universities, a few teachers, and the education department. At the in-service courses that were held early this year, (referred to above) comments from and involvement of teachers, were invited. Anyone interested to be involved had the opportunity to join this process. However the Education Department bears final responsibility for the document, and the process that was set up to draft it. What makes this relative openness possible and desirable, I believe, is the ethos of the new political dispensation which promotes the values of greater transparency and accountability to the public. It is also to the credit of the individuals involved.
REMESA, while accepting and participating in the Western Cape formulation of the official curriculum, and in presenting these in-service courses held by the partnership, has a particular ideal, which it is in the process of developing and researching. In our case, we negotiate with the teachers of project schools to implement our `intended curriculum'. They are allowed the freedom to create their own version which they regard as implementable. The pupils, as always, attain certain parts and variations of this implemented curriculum.
What we are in the process of recording, are:
Would it help, then, to write the intended curriculum in the form of textbooks and other materials? Yes certainly, but it has still to be interpreted by the teachers themselves, and again, they will tend to only accept what `chimes with popular memory', and continue to teach in the manner they have always taught. As Muller and Taylor put it: `The handing over of the finished products syllabuses and textbooks to the teachers for implementation is based on an epistemology that underlies all forms of authoritarian canonization' ... `Syllabus plus textbook equals curriculum. Curriculum is presumed to be transparent: teachers (and in some instances pupils) should only have to read it for all to be clear...once the knowledge has been extracted from the text, the means of translating this into classroom practice is also supposed to be automatic.' (Taylor (1993) p 321).
The two processes, then, that should be studied concerning curriculum change, are both: the `top-down' process of `legislating' a curriculum, (of which textbooks written in accordance, may be a component) and the `bottom-up' process of teachers evaluating the effectiveness of their own teaching, and demanding support in the process of change. Linking these two processes, are other processes, such a mediation, consultation, facilitating change in the classroom... These latter processes are complex, and they are the task of a variety of education workers, acting as `change agents', some of them teachers themselves, others advisors from the Education Departments, or academics.
The `legislated' curriculum might, somewhat ironically, help to facilitate change in the classroom where teachers are used to obeying directives from an education department. Likewise, textbooks which encourage a new methodology, could assist in the process, (but not stand alone) because the authority of the textbook is seldom questioned. This is a paradox that one should use exaggerated respect for authority to create a questioning culture in the classroom. Such are the types of interesting dilemmas these `facilitation' processes involve.
It is understandable that they tend to underestimate what children are capable of, judging only by what can be observed in the restrictive classroom environment. Jan De Lange also relates (p 47, 59) how, in studying mathematization in The Netherlands, it was found that problems that were too `difficult' to solve in classroom conditions, with restricted time, could be solved very satisfactorily for homework. The tendency for adults to use their acquired, formalized knowledge, also plays a role in teachers' perceptions of the level of difficulty of classroom activities. There is an example in De Lange (p 78), where teachers were hindered by their `context-isolated' knowledge of logarithms, from solving a problem which students did not find problematic.
Below are descriptions of lessons or moments in lessons, given to `standard 6' (grade 8) pupils. The lessons were given at the beginning of this year, around the syllabus topics under the heading `Lines and Angles'. The lesson material which we prepared, covered a whole quarter's worth of geometry (one of four sections of the syllabus). A detailed lesson plan was provided, with most lesson suggestions also outlined in some detail. It attempted to integrate `vision geometry' (a realistic mathematics education approach) with the more conventional interpretation, including investigative activities. The whole package was relatively innovative in the sense that the activities were intended to be done in an exploratory way by the pupils themselves. We held an intensive weekend workshop beforehand to provide teachers with the opportunity to work through the activities and discuss them.
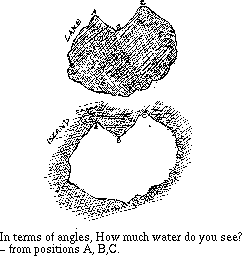
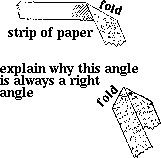
I observed a lesson where the teacher gave clear instructions, and from where I sat and observed, all seemed to be going well. When I walked around the class however, the strips of paper had been folded at random, and the pupils had clearly all been calculating supplementary angles in degrees already. They indicated that they thought the activity senseless.

The vision geometry activities were perceived by the teachers as being too `time-consuming' and they were postponed to be done later in the year. Thereby perhaps politely indicating that they regarded these activities as just a bit of fun to enrich children's learning. This was disappointing as we had integrated the more familiar with the less familiar activities by design. But indications are that they could have been feeling insecure about their mathematical understanding of these activities, as well as the particular didactical demands involved.
Bob started by demonstrating different angles by rotating his forearm at the elbow. The children listened and imitated the movements. He showed them a right angle in this way (his upper arm horizontal, his forearm pointing upwards). Then he wrote on the board: `a right angle =  '. The children had to write in their exercise books what they thought a right angle is. He paused long enough for them to write something, then asked a few children to tell their answers. Examples of answers: `90 degrees'; `an angle with 2 sides'; `when a vertical and horizontal line meet'.
'. The children had to write in their exercise books what they thought a right angle is. He paused long enough for them to write something, then asked a few children to tell their answers. Examples of answers: `90 degrees'; `an angle with 2 sides'; `when a vertical and horizontal line meet'.
Bob took the opportunity of this last reply to make an important point, anticipating the misconception that these angles can only have one particular orientation. He drew a vertical and horizontal line on the board, while conducting a dialogue with the class. He then drew another right angle in a different orientation and asked whether that is still a right angle. Everything he said, was phrased as a question, even when the answer was obvious. (This being a commonly employed technique which holds the pupils' attention very well.)
The rest of the lesson proceeded in a similar way. With each type of angle, Bob asked a question, while demonstrating with his arm, received an answer from the most alert pupils, wrote the term on the board, and each pupil then had to formulate their own definition. Then he walked around, asking for the answers, and reacted to them. He accepted any answer which was not totally incorrect, and gently but firmly corrected incorrect answers. He probably interacted with every child in the class in the course of the lesson.
The pupils worked alone, never getting the opportunity to discuss with a neighbor. Through the reading out of answers, they did get the opportunity to share their versions with the whole class. Everything proceeded in a very orderly way, as seems usual with this teacher's classes, but the children also seemed to enjoy the lesson and paid complete attention.
The pupils had two ways to respond to the question of the definition of each type of angle: calling out, or writing. Interestingly, they seemed to prioritize the writing. They eventually started writing down their definitions without being told, and before they had called out any answer. They knew their teacher would take their written answers seriously, rewarding them with attention. It also seems significant that they had the freedom to find their own words for describing the terms.
The lesson was not only about the names for different types of angles, but also about the skill of classification as a way of organizing concepts. Bob demonstrated clearly that every term refers to a range of different angles, and by asking for their definitions, was allowing the children to classify many different angles into every category, for themselves. Moreover, because of the coherence of the lesson, the children could predict the next question, and already start to answer it. There was thus a level of participation which was not superficially apparent. Some children gave an angle size in degrees instead of a definition. Perhaps Bob could have insisted on a definition, or perhaps the children understood that if all their answers are valid, a general category is involved. I do think that by the end of the lesson most of the children did understand this.
In this lesson, as in the others described here, there are none of the trappings that seem to be fashionable, indicative of `problem solving' or `investigation', i.e. group work or pair work, a fair level of noise, attractive apparatus or worksheets, the pupils left to work on a problem for some time on their own. Yet I believe there was skilful facilitation of learning happening in this classroom.
To assess quickly whether the pupils could recognize the terms, Bob eventually walked through the class, asking each pupil a question, such as `what type of angle is this' or `show me an obtuse angle'. He thus had a fair idea by the end of the lesson, of who had mastered the recognition of angles. Also, from the written aspect of the lesson, he had an impression of the insight various pupils might have, or lack. For me, he demonstrated how to handle a large class in a relatively confined classroom, ensure that most pupils learn something, assess his pupils' knowledge (albeit superficially), and give many of them an opportunity to produce something on their own and that in 50 minutes!
This teacher (let us call him Sam) invented two models to illustrate angle types, after he did the `arms' lesson: he held up two rulers meeting at an angle. This was particularly useful in the discussion of the `straight' angle he stressed and repeated, that there still has to be an identifiable vertex even where the angle is `straight'. Yet another analogy that he thought of was that when the hands of a watch form a straight line, they are still attached to each other, the vertex remains at exactly the same place.
He then proceeded to reflex angles. The context that he had thought of here, as an alternative to the `island' and `lake' idea, was `Pacman', the computer game that a number of children might be familiar with, and enjoy. Pacman is a character with a circular shape which has a sector missing. This sector varies in size, making it look like a mouth which opens and closes. It is moved over the screen `eating' everything in its path. The teacher referred to the game without further description. Most of the time `Pacman's' mouth forms an acute angle. Having briefly mentioned this, the teacher changed the context brilliantly: `Imagine Pacman is a swimming pool the `inside' is now where the water is a reflex angle is formed at the vertex where we saw an acute angle before.' Another sketch on the board... this time of the fence around a garden: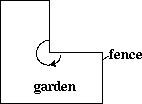
The teacher said: `Although it looks as though it is outside of the angle, it is still on the inside'. At this point the children appeared uncertain, but none asked a question and Sam did not check whether they understood. Finally we arrived at the concept of `revolution' (360 degree angle). He drew it on the board, with the remark: `This is still the `inside' of my angle!'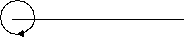
This idea of `inside' and `outside' an angle, was inspired by our materials. This teacher invented analogies with which the children would identify, to serve the same conceptual purpose. One problem with this is that Pacman and the swimming pool have nothing in common, whereas the island and lake are both geographical features, which one can imagine as occurring in the same plane. Pacman's mouth changes size all the time (as such it is a good context for angles) but the swimming pool's angle remains fixed. On the other hand, the wide variety of illustrations would have served to encourage generalization, if the teacher had given the pupils a chance to formulate their own descriptions.
The lesson in general took our ideas and attempted to improve on them. Sam had got the message that relating mathematics to the children's everyday lives would serve to motivate and interest them. He also got the message that he himself was expected to be innovative he seemed to think that simply following our ideas would contradict our encouragement in this regard. He presented a variety of contexts to illustrate the concepts indeed the best way to ensure a proper definition. Thus some of the express aims of our work were satisfied by this lesson.
Sam did the demonstration with arms in a horizontal plane, as we had conveyed the idea to the teachers. In classes where the activity was translated to the vertical dimension, there is a danger, as before, of the misconception of regarding only certain orientations of angles as conforming to the definitions. Even Sam drew all his angles on the board with one line segment horizontal, and the angle opening up towards the top of the board. Another teacher who rushed this lesson, did the demonstration in both ways. Although there is nothing wrong with this per se, his pupils got confused when demonstrating the reflex angle, thinking that the elbow always has to be thrust backwards, even when the angles are demonstrated in a vertical plane.
The relative importance that was accorded this topic by all the teachers, out of proportion to its mathematical significance, is a problem of the official curriculum. It creates the impression, especially by the way topics are listed, that knowing the terms are the most important feature of the subject, and that the topics and terms are all equally important. This impression has been reinforced over the years by textbooks, teacher training, and the fact that it is easier to assess knowledge of terms than anything else. The deliberate design of this activity as preparation for other activities, and to prevent misconceptions, seemed mostly lost on the teachers.
Establishing links among different parts of the syllabus, is also discouraged by the fragmented way in which the topics are listed in the syllabus, and these teachers are only beginning to consider covering a few small topics under one theme (e.g. topics related to triangles and parallel lines, via tessellations). A telling detail of Sam's lesson, worth keeping in mind for future discussion with the teachers, was that in the course of revising the types of angles, Sam said: `angles cannot be less than 0 degrees, because 0 is nothing.'...
Nonetheless, the teacher himself demonstrated adaptability, by changing one context into another, and by the creative thoughts that went into planning the lesson. Sam's teaching would benefit from an awareness of anticipating and exploiting apparent contradictions such the `inside/outside of an angle'. Most of all, what is needed is the willingness to let go, to hand over the action of exploration to the pupils themselves, and to give them the opportunity to express their own ideas based on their own intuitions.
As with the other two lessons described, Peter uses a didactical method involving dialogue with the whole class. His interaction with the class is not as tightly controlled as that of Bob, and he does allow unpredictable responses from his pupils, in contrast to Sam. Peter received help from myself in planning the lesson, but the manner in which he conducted it, is all his own innovation.
Peter drew two intersecting lines on the board, placed a transparency sheet over them and traced them, using a ruler. Then he `translated' the drawing upwards, along one of the lines. And asked: `What do you notice?' The children did not know what to answer, but seemed to think it must be an easy answer, and shouted out various answers such as: `vertically opposite!', `The lines are straight', `180 degrees!', `The line becomes longer!'
With every attempt, Peter acknowledged the answer, saying `you're right but what else?'
Then he asked: `How many angles are here?'
`8', they said.
This gave them a hint somehow, and someone shouted: `corresponding angles!'
That was what he wanted.
Peter: `What other pairs of angles do you see?'
Many children now seemed to remember the other names for angle pairs associated with this type of sketch.
The next question, and the dialogue that follows, were improvised by Peter as he went along.
Peter: `If I shift it here, do I get the same pairs?' (translating the sketch along another line.)
There were a variety of responses...
Peter: `Who says `Yes'? Who says `No'?...'
A pupil shouted `who says maybe!'
Peter: `Who says `maybe'?'
It turned out that most of the class was unsure.
He demonstrated further, to resolve the conflict.
Peter: `Are there other corresponding pairs? How many corresponding pairs?'
Class: `2'
He demonstrated and the class counted with him. (Generally the class was paying close attention, which is not always the case with this teacher.)
Gradually the class became convinced that there were in fact 4 pairs.
Peter: `Are you sure there are 4?'
Peter did the same with the alternate and cointerior angles, where it was clearer that there were only 2 pairs each.
Peter then went on to demonstrate rotation, asking: `What do you notice?'
`Alternate angles!' they said.
This time they knew what he was after.
Peter: `Are these 2 angles the same?'
Class: `Yes'
Peter: `Why are they the same?...'
He gave the explanation himself, but the fact that he did ask `Why', and paused, was very significant not only in the context of the predominant ways of teaching (as can be seen from lessons 1 and 2) but also in the context of his own teaching. His explanation moreover, was very visual, and appealed to intuition rather than verbal reasoning. It was interesting that the activity seemed to urge him to explain in such an unusual way.
Peter: `Do we have corresponding angles?'
Class: `Yes'
Peter: `Vertically opposite angles?'
Class: `Yes'
Peter: `Adjacent supplementary angles?'
(Again improvising)
Class: `No' (or unsure)
Peter picked up on this doubt and asked `who says `yes', `no', `unsure'?...'
Only one child said yes. Even after he pointed in the sketch to 2 adjacent supplementary angles, saying `here is a straight line', they were still not convinced. (Evidence that one of the previous lessons with paper folding was unsuccessful.)
Pater: `Well I will tell you the answer: there are adjacent supplementary angles.'
He left it at that.
Peter generated interest in this mathematics lesson by getting the children to have an opinion. It is perhaps the beginning of what Alan Schoenfeld refers to as a `mathematical community' in the classroom (1989, p 16). The pupils are encouraged to make simple reasoned conjectures, and in this case, compete through a kind of `voting' procedure. Peter, in contrast to the other teachers, dares to ask open-ended questions, like `what do you notice?' and accepts a number of answers to these.
Department of Arts, Culture, Science and Technology (1996). South Africa's Green Paper on Science and Technology Preparing for the 21st Century. January 1996.
Department of Education (1995). `Education White Paper1'. Pretoria, November 1995.
Department of Education (1996). `Education White Paper2, General Notice, Notice 130 of 1996, The Organisation, Governance and Funding of Schools'. Pretoria, February 1996.
De Lange, J. (1887). Mathematics Insight and Meaning, Teaching Learning and Testing of Mathematics for the Life and Social Sciences. Vakgroep Onderzoek Wiskundeonderwijs en Onderwijscomputercentrum, Rijksuniversiteit Utrecht, Utrecht.
Freudenthal, H. (1968). `Why to Teach Mathematics so as to be Useful'. Educational Studies in Mathematics, 1, 38.
Freudenthal, H. (1973). `Geometry Between the Devil and the Deep Sea. Educational Studies in Mathematics, 3, 413435.
Gravemeijer, K.P.E. (1994) Developing Realistic Mathematics Education (Doctoral dissertation). Utrecht: CDbeta Press / Freudenthal Institute.
Schoenfeld, A.H. (1989). Reflections on Doing and Teaching Mathematics, Paper presented at a conference "Mathematical Thinking and Problem Solving", Berkeley, CA, December 1989.
Streefland, L. (1988). Realistisch breukenonderwijs (Dissertatie). Utrecht: OW&OC, Utrecht University.
Taylor, N. (1993). Inventing Knowledge: Contests in Curriculum Construction. Maskew Miller Longman, Cape Town.
Travers, K.J. (1986). Second International Mathematics Study Detailed Report for the United States, Stipes Publishing Company, Champaign, Illinois.
Van den Heuvel-Panhuizen, M. (1996). Assessment and Realistic Mathematics Education. Utrecht University, Utrecht.
Western Cape Education Department (1996). Draft Syllabus for Mathematics, Standards 5 to 7. Unpublished.
Generated with CERN WebMaker