Ja. Neem eerst a1 = 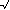 2
en b1 =
2
en b1 = 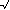 2. Nu zij er twee mogelijkheden:
2. Nu zij er twee mogelijkheden:
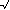 2
2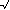 2 is wel of is niet
rationaal. In het eerste geval is de vraag beantwoord. In het tweede geval is
dus
2 is wel of is niet
rationaal. In het eerste geval is de vraag beantwoord. In het tweede geval is
dus 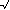 2
2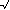 2 niet-rationaal.
Maar neem dan als niet-rationale getallen a2 =
2 niet-rationaal.
Maar neem dan als niet-rationale getallen a2 = 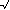 2
2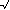 2
en b2 =
2
en b2 = 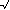 2 met als resul-taat: (
2 met als resul-taat: (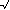 2
2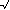 2)
2)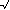 2
= 2 is rationaal! Is nu de vraag beantwoord? Er is aangetoond dat ze er zijn,
maar a en b zelf zijn niet gevonden.
2
= 2 is rationaal! Is nu de vraag beantwoord? Er is aangetoond dat ze er zijn,
maar a en b zelf zijn niet gevonden.
De Nederlandse wiskundige Brouwer is de grondlegger van de theorie waarin dergelijke bewijzen niet zijn toegestaan. Deze theorie stamt uit het begin van deze eeuw en heeft tegenwoordig veel toepassingen in de informatica. Het begrip `bewijs' blijkt niet meer absoluut vast te liggen.
Het bewijs van het vierkleurenprobleem is lang en onoverzichtelijk omdat circa 2000 kaarten gecontroleerd moeten worden. Praktisch gezien kunnen alleen computers dit nagaan. Wat betekent dat voor bewijzen? The death of proof was de enigszins demagogische titel van een artikel in de Scientific American (oktober 1993). Het bewijzen als een creatieve activiteit om een logisch en overzichtelijk pad te vinden vanuit axioma's naar een onweerlegbare stelling, leek achterhaald.
Het bleek minder ernstig. Wiskundigen moesten zich eens gaan realiseren dat het bewijzen plaats vindt in een sociale context. Wat onweerlegbaar is, is ook sociaal bepaald en mogelijk tijdelijk. Hoewel in het slot van het artikel iemand waarschuwt dat het niet erg bemoedigend zou zijn als in de toekomst een computer antwoordt op de vraag of een hypothese correct is: `Ja, het is correct, maar je zult het bewijs niet begrijpen.'
Bewijzen moet - maar hoe (en waarom)?
Prof.dr. D. van Dalen
Faculteit Wijsbegeerte, Universiteit Utrecht
Vrijdag 13.30-14.15 uur
Het karakteristieke van wiskunde is dat de eisen aan zekerheid ver uitgaan boven die van de andere wetenschappen. Bijvoorbeeld, waarom is `7 is een priemgetal' van een andere zekerheid dan `de standaardmeter in Parijs is 1 meter lang'? De wiskundige zekerheid is het resultaat van onze bewijsactiviteit. Geen bewijzen, geen wiskunde. We zullen ingaan op het begrip `bewijs' en op de didactische problemen die aan de noodzaak van bewijzen en aan de techniek van bewijzen kleven. Zelfs al kunnen we in de praktijk van het onderwijs niet geheel voldoen aan de strengheidseisen die de moderne wiskunde stelt, het is van het grootste belang dat over de principiële strekking geen twijfel bestaat.
Debat: Bewijzen in het wiskundeonderwijs?
Henk Barendregt en Aad Goddijn
Katholieke Universiteit, Nijmegen en Freudenthal instituut, Universiteit Utrecht
Een punt van discussie is nog altijd de vraag hoever je moet gaan bij het inzicht geven aan leerlingen in wat een bewijs is, in het bijzonder in het iets tonen van de formele aspecten van het bewijsbegrip. Het standpunt zou verdedigd kunnen worden dat juist het begrip bewijs in onze intellectuele traditie z'n betekenis ontleend heeft aan de wiskunde.
Maar als je naar de geschiedenis van de wiskunde kijkt, is het niet toevallig dat bewijzen een aanschouwelijke oorsprong heeft.
De opzet van dit debat is om deze contraverse verder te onderzoeken. Daartoe zijn twee combattanten uitgenodigd die in een exploratief twistgesprek de vraag zullen verkennen, uitgaande van een zo helder mogelijk geprofileerde controverse.
Redeneren leren als formeel spel
Prof.dr. N.G. de Bruijn
Technische Universiteit Eindhoven