|
Een ander gebied waarop grafieken een zekere rol
hebben gespeeld was het onderzoek naar zaken als de samenstelling en de groei van bevolking van een land;
dit soort onderzoek vormde vanaf de 17e eeuw een belangrijke
impuls voor de ontwikkeling van de statistiek. We zagen al eerder dat Chr. Huygens
een van de pioniers was op dit terrein.
Een van de eersten die in dit verband systematisch grafieken toepaste
was J.L. d'Alembert (1717-1783), maar hij beperkte zich tot hypothetische
grafieken die niet gebaseerd waren op reële gegevens. |
Klik op het plaatje om de grafiek
te kunnen zien |
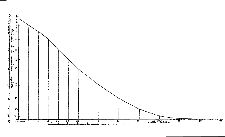
De wiskundige J.B.J. Fourier (1768-1830)
maakte uitgebreide grafieken van de resultaten van de Franse volkstelling
van 1817. In een artikel uit 1821 gaf hij de leeftijdsopbouw van de mannelijke
bevolking van Parijs weer in wat waarschijnlijk de eerste cumulatieve frequentiekromme
is geweest (zie de figuur hiernaast).
Hij legde onder meer uit hoe deze grafiek kon worden
gebruikt om bijvoorbeeld af te lezen hoeveel mannen er waren tussen twee leeftijdsgrenzen. |
|
In 1828 publiceerde de Belgische wetenschapper
Lambert Adolphe Jacques Quetelet grafieken waarin hij empirische gegevens over de
sterfte in België vergeleek met die in Frankrijk.
|
|
Over Quetelet (1796-1874) heeft Ida Stamhuis onlangs
een uitvoerig artikel in Euclides geschreven (Stamhuis 1996a). Quetelet,
van oorsprong wis- en sterrenkundige, begon zich te interesseren voor de
statistiek, en dan vooral de sociale statistiek. Hij was betrokken bij de eerste grote volkstelling, die in 1830 plaatsvond in de
toenmalige Nederlanden. Quetelet ontwikkelde het idee van de 'gemiddelde
mens' en modelleerde menselijke eigenschappen (zowel lichamelijke als geestelijke)
m.b.v. de normale verdeling, die hij kende uit de foutenanalyse in de sterrenkunde. |
Uit 1827 stamt de grafiek die hiernaast
is afgebeeld, waarschijnlijk een van de eerste voorbeelden van de grafische
weergave van het chronologisch verloop van bevolkingsgegevens.
In de grafiek zijn het aantal geboorten en sterftes
in Brussel, per maand - gemiddelden over een periode van 18 jaar - uitgezet,
samen met het temperatuurverloop. De afwerking van de grafiek is tamelijk
simpel, een verticale schaalverdeling ontbreekt. |

klik op het plaatje om de grafiek
(iets)
beter te kunnen zien |
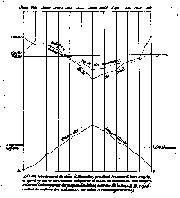
In een andere grafiek (zie hiernaast) maakte Quetelet een vergelijking
tussen het aantal geboorten, sterftes en huwelijken in de verschillende
Nederlandse provincies (waar in 1827 ook België nog onder viel).
In de grafiek zijn opgenomen: de verhouding bevolking
: aantal sterfgevallen, bevolking : geboorten, bevolking : huwelijken en
geboorten : huwelijken.
Quetelet is waarschijnlijk ook de eerste geweest
die gebruik maakte van frequentieverdelingen.
Hij tekende een grafiek waarin
hij het percentage misdaden begaan in elke leeftijdsgroep weergaf.
|
| Quetelet was ook de initiatiefnemer van het eerste
internationale Statistische Congres, dat in 1853 in Brussel werd gehouden.
Op dit eerste congres volgden tot 1876 nog acht andere. Op het derde congres
(Wenen, 1857) werd de grafische weergave van statistische gegevens uitgebreid
besproken en er ontstonden heftige discussies, o.m. over de vraag
of de grafische methode wel wetenschappelijk was. Op de volgende congressen
kwam het onderwerp regelmatig terug, en werd o.m. gestreden over de vraag
in hoeverre het Congres aanbevelingen moest doen over de standaardisering
van grafieken. (zie: Funkhouser 1937, p.
310 e.v.) |








